Matemáticas fronte a 2ª lingua
Elhuyar: De onde chegou a este tema?

J. F. L.:
Non foi un tema que se expuxo bruscamente; antes de ser profesor da Universidade impartía clases de matemáticas nunha Ikastola do modelo B. Eran alumnos de ciclo superior e o salto ao Ensino Medio era inmediato. A pesar de que estes alumnos traballaban as matemáticas en castelán, a intención dos profesores era integrar o maior número de alumnos no modelo D do Ensino Medio, non era ilóxico pensar que podían ter problemas. Esta investigación iniciouse na crenza de que era urxente verificar, analizar e clasificar esta previsión.
PaP: Cales son os obxectivos deste traballo?
J. F. L.:
Un dos principais obxectivos expostos por nós era establecer as bases científicas paira reformular o ensino de maneira que os alumnos do modelo B non tivesen problemas paira traballar as matemáticas en eúscaro ao incorporarse ao modelo D no Ensino Medio. Antes, con todo, había que analizar si tiñan ou non problemas, xa que podía ser posible que non houbese ningún problema e que o noso fose una mera sospeita.
O obxectivo do modelo B está claro: Capacitar para que calquera alumno de 8º curso poida seguir calquera tema tanto en eúscaro como en castelán, para o que cada centro porá os medios necesarios. Segundo esta formulación teórica, ao pasar ao Ensino Medio non terían inconveniente nin no castelán nin no eúscaro, pero as cousas case nunca suceden así (e eu refírome ás matemáticas, que é o noso tema de estudo), entre outras cousas, porque nalgúns centros trabállase as matemáticas que estudamos en castelán.

O obxectivo principal desta tese estaría relacionado con esta preocupación: É dicir, se se cumpre ou non o obxectivo marcado polo modelo B, e como afecta o alumnado en caso de incumprimento.
PaP: Por que estudar o binomio matemática/linguaxe?
J. F. L.:
Aínda que pareza que as matemáticas e a lingua están distanciadas, en calquera proceso de ensino (incluídas as matemáticas), a influencia da lingua é innegable. Como di Sánchez Carrion no seu libro Un futuro paira o noso pasado, o profesor está a ensinar calquera tema, pero sempre está a traballar o idioma. Por tanto, querer analizar as relacións entre as matemáticas e a lingua non resulta tan estraño.
En contextos bilingües o problema agudízase, xa que paira ser verdadeiramente bilingüe é necesario ser capaz de utilizar ambas as linguas en calquera tema, mesmo en matemáticas. Aquí empeza a xurdir problemas reais, xa que isto non se cumpre do todo no modelo B.
O uso de ambas as linguas, pola súa banda, non debería impedir en ningún caso a asimilación das diferentes materias, cousa que ninguén admitiría. En calquera programa, sexa monolingüe ou bilingüe, establécense uns obxectivos mínimos aos que hai que chegar, aínda que cada centro teña liberdade paira elixir metodoloxía, material, recursos, etc. Se ademais de conseguilo chega a dominar a 2ª lingua ou a 3ª, mellor.
A pesar de que teoricamente era así, pensabamos que era interesante saber que pasa realmente e a iso puxémonos en marcha; analizar se o ensino bilingüe supón un obstáculo paira a asimilación dos contidos matemáticos.
PaP: Até que punto a linguaxe pode condicionar o proceso de introdución das matemáticas?
J. F. L.:
Como se mencionou anteriormente, a linguaxe condiciona o ensino de calquera materia, e as matemáticas non quedan fóra desta regra xeral. Até agora falamos das matemáticas na súa totalidade, pero, seguindo a taxonomía de Bloom, convén diferenciar diferentes procesos como o cálculo, a comprensión e a aplicación. En cada una destas linguas inflúe diferente. A importancia da linguaxe simbólica no cálculo é: 3x4=12 é facilmente comprensible en calquera idioma, por suposto, cuns coñecementos matemáticos mínimos. Sen faltar demasiado, pódese pensar que os do modelo B non terán demasiados problemas neste proceso, pero si no desenvolvemento da comprensión, é dicir, na comprensión das manifestacións do profesor ou dun texto escrito. Na aplicación, é dicir, na resolución de problemas, cobra especial importancia a linguaxe.
Estes dous últimos procesos serán os que teremos que analizar especialmente, xa que neles inflúe sobre todo a linguaxe, e no noso caso, ao falar da lingua 2, non da lingua materna, parecíanos que podía haber problemas.
PaP: Cal é actualmente o B.Ou.P.V. e a organización do ensino das matemáticas na Ou.B.I?
J. F. L.:
Na Comunidade Autónoma Vasca distínguense tres modelos lingüísticos:
- Modelo A, especialmente dirixido a nenos erdaldunes. Todo se ensina en castelán e entre outros obxectivos mínimos estaría a aprendizaxe do eúscaro; aprender “eúscaro” e non “eúscaro”.
- O modelo D, onde todo faise en eúscaro, co castelán como materia.
- Por último, atopámonos co modelo B que estudamos, no que o eúscaro e o castelán son tratados teoricamente polo menos ao mesmo nivel, pero traballan as matemáticas, a escritura e a lectura en castelán, mentres que o resto de materias impártense en eúscaro. Por que ocorre así? Nalgunhas teorías e estudos demostrouse que para que non haxa atrasos nestes temas importantes é necesario tomar os conceptos básicos na lingua materna.
Aínda que no B.Ou.U. diferéncianse estes tres modelos, non ocorre o mesmo no Ensino Medio, xa que aquí só hai dous modelos, os modelos A e D. En teoría, os alumnos do modelo B. Una vez terminada, xa estarían preparadas tanto paira o modelo A como paira o modelo D.
É capaz o alumno de empezar a traballar as matemáticas en castelán até o 8º curso? Non vai explicar atraso respecto dos que aprenderon eúscaro?
PaP: Pero cando se dá ese paso, que é o que máis inconveniente supón: os cambios lingüísticos ou as dificultades do tema?
J. F. L.:
Ambos teñen importancia e ambos van unidos. Calquera podería pensar que non sería máis que una falta de costume, una falta de costume que se superaría tras uns meses mal. En parte é así, pero non só iso.
No Ensino Medio os conceptos e contidos complícanse esixindo un maior desenvolvemento lingüístico. Os modelos D ou A tamén poden ter este problema, pero o desfasamento que poden ter os demais é máis grave. Creemos que aínda que á hora de analizar as conclusións imos concretar máis, o cambio lingüístico debería facerse antes de pasar á RCP.
PaP: Como expuxestes o estudo empírico?
J. F. L.:
Até agora tratei de dar conta da formulación teórica, pero este traballo non foi una mera teorización. Á hora de deseñar o estudo pareceunos que tiñamos que facer catro grupos diferentes de 8º curso:
Grupo formado por un número de alumnos do modelo A (grupo A) con alumnos do modelo B, dous grupos (grupo B e grupo B) outro grupo do modelo D (grupo D)
A e B pasamos as probas en castelán e a D e B’ en eúscaro. Dado que o noso estudo estaba dirixido ao modelo B, aquí tiñamos a oportunidade de comparalo con dous grupos en eúscaro e castelán: Grupo B coa e B’ con D.
Paira completar a mostra, acudimos aos colexios públicos e ás ikastolas da Comunidade Autónoma Vasca co obxectivo de conseguir uns 900 alumnos. Non fomos aos centros privados, entre outras cousas porque en Álava non atopamos polo menos D.
As variables consideradas serían, por unha banda, a propia matemática como variable dependente (distinguindo o cálculo a abordar dentro das matemáticas, a comprensión dunha explicación, a comprensión e aplicación do texto escrito) e, por outro, o nivel de eúscaro que consideramos como variables independentes, o tipo de centro, o modelo lingüístico, o nivel socioeconómico, a idade, o sexo, etc.
PaP: Como medistes o nivel de matemáticas?
J. F. L.:
Utilizamos tres probas diferentes paira medir coñecementos matemáticos:- Test estranxeiro EIA ( International Evaluation Achievement ) de Estados Unidos. Partindo da versión en castelán, antes de pasar aos alumnos, tiñamos que traducir, validar e controlar a fiabilidade. Leste foi o primeiro paso. Esta proba consta de 40 ítems que recollen contidos do nivel 8: xeometría, fraccións, aritmética,... Con esta proba mídense catro procesos diferentes: cálculo, comprensión, aplicación e análise (os relativos á análise son só dúas ítems e ao non ter influencia significativa na investigación apenas se tiveron en conta).
- Paira poder medir a comprensión da exposición do profesor, un profesor da RCP, tras pasar una explicación previamente gravada en vídeo, preguntámoslles sobre ela. A duración do vídeo é de hora e media e, por suposto, tivo dúas versións, una en eúscaro e outra en castelán.
- Paira medir a comprensión do texto escrito, seleccionouse o tema da probabilidade do libro BBB-1 publicado por Elhuyar. Non completa, é demasiado longa. Dado que o texto atopábase en eúscaro, traduciuse ao castelán paira pasar aos grupos A e B. Tras ler o texto había que responder a varias preguntas, unhas en eúscaro e outras en castelán.
Tanto á hora de elixir a proba de probabilidade como á hora de elixir a de vídeo, limitáronnos dúas condicións principais: por unha banda, o feito de que o tema sexa novo, xa que de ser tratado previamente os resultados serían “non reais”, e doutra banda, o feito de que sexa un tema a nivel de desenvolvemento do alumnado.
Paira medir variables independentes, tivemos que crear algunhas probas, pero non todas, como o test estandarizado D-48 que utilizamos paira medir a intelixencia. A proba que creamos é a adaptación ao conto Peru makur. Nesta proba na que tras a lectura do conto aparecen as preguntas que lle corresponden, medirase o seu nivel de lectura en eúscaro. Mídense principalmente tres aspectos: velocidade de lectura, porcentaxe de comprensión e porcentaxe de velocidade de lectura.
A nova ferramenta supón a realización dun traballo “extra” previo á súa incorporación á investigación real, como a realización da mesma proba e o control de fiabilidade e utilidade. Una vez feito isto, estaría disposto a pasalo.
PaP: As ferramentas de medición utilizadas por vós son utilizables por calquera profesor?
J. F. L.:
En xeral si, aínda que algunhas probas foron especialmente preparadas paira esta investigación (Vídeo proba, texto utilizado paira medir probabilidades e proba baseada no conto Peru makur). O resto, con todo, é accesible paira calquera persoa, a condición de que o nivel dos alumnos sexa 8 ou superior (test EIA, test D-48 e conto Peru makur).
PaP: Cal sería a conclusión máis destacable?
J. F. L.:
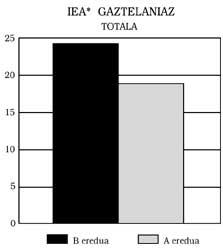
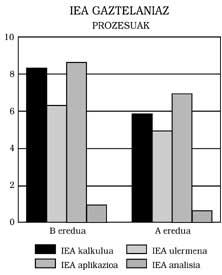
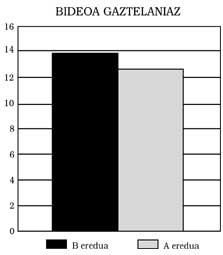
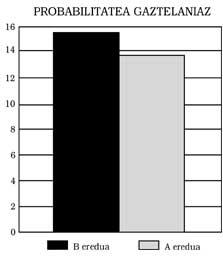
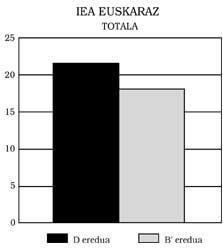
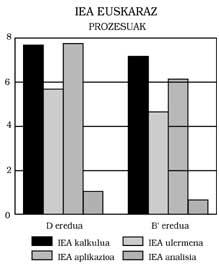
Pódense extraer tres conclusións principais: 1) Os alumnos do modelo B presentan ao responder en castelán un nivel mínimo equivalente ao dos do modelo A. Isto significa: Os do modelo B non mostran ningún atraso matemático, aínda que o modelo de ensino sexa bilingüe. Máis aínda, como se pode observar nas Figuras 1, 2, 3 e 4, obtiveron mellores puntuacións que as do modelo A. Nalgúns casos, ademais, as diferenzas foron estatisticamente significativas, pese ao control da intelixencia e do nivel socioeconómico. Calquera podería pensar que a mellor puntuación é a promovida polo efecto beneficioso do bilingüismo, pero non nos atrevemos a dicilo. Una investigación máis profunda, que non foi una das nosas metas.
A razón real desta diferenza entre os modelos A e B, tal e como analizamos, estaría no tipo de centro. Mentres no modelo B atópanse as ikastolas e os centros públicos, no modelo A só os centros públicos (nas ikastolas non hai modelo A). Por outra banda, o contexto no que se sitúan os centros públicos do modelo A adoita ser marxinal, no que se presentan abundantes e frecuentes problemas de integración, adaptación, etc.
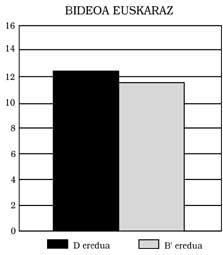
Esta pode ser a razón principal desta diferenza. 2) Comparando os do modelo B’e D, en todas as probas mostráronse os do D por encima (ver figuras 5, 6, 7 e 8 paira iso). Estas diferenzas son significativas en aspectos como a aplicación e a explicación dun profesor ou a comprensión dun texto, pero noutros como o cálculo non ocorre. Cal é a súa explicación? Ao ter un maior nivel lingüístico, naqueles casos nos que a influencia da lingua é elevada, os do modelo D obteñen mellores resultados. 3) A terceira conclusión é que se contrastaron os resultados obtidos noutros contextos bilingües, é dicir, que canto máis se traballou e utilizado a segunda lingua na escola, maior é o grao de competencia, sen que a primeira lingua sufra ningún atraso.
Que pasou no noso caso? Observamos diferenzas significativas entre os modelos B. En calquera caso, cando falamos do modelo B, hai que dicir que se trata dun modelo moi xeneralizado, xa que se poden atopar modelos B máis euskaldunes e castellanoparlantes. Esta clasificación realízase en función de tres variables: porcentaxe de euskaldunes entre profesorado, porcentaxe de materias do ciclo superior que se cursan en eúscaro, e por último, a partir do curso 6, traballar as matemáticas en eúscaro ou en castelán.
A diferenza entre os modelos B é real, xa que nas probas matemáticas o modelo B máis euskaldun obtén una mellor puntuación. Ao pasar a proba en castelán apenas houbo diferenzas. En definitiva, o que se consegue coa lingua nalgúns contextos bilingües, conseguímolo coa matemática, é dicir, canto máis traballemos as matemáticas na segunda lingua, máis competencia é na segunda lingua sen atrasos na lingua materna.
A verdade é que estes resultados non fixeron crer demasiados imprevistos en nós, talvez a maior das imprevistos sexa a diferenza entre os modelos B e A, que esperabamos resultados inversos. Dixemos, con todo, cal pode ser a súa razón.
PaP: Como reestruturariades o ensino ante estas conclusións para que os resultados sexan ‘óptimos’?
J. F. L.:
De acordo co visto, en primeiro lugar modificaríase a estructuración das matemáticas no modelo B, polo menos no que se refire ao uso da lingua (se se quere alcanzar o obxectivo principal ao que se fixo referencia, que una vez finalizado o nivel 8, sexa capaz de cursar os seus estudos tanto en eúscaro como en castelán). Paira iso é necesario que a partir de certo nivel comécese a traballar tamén as matemáticas en eúscaro, e como dicimos nas implicacións pedagóxicas da tese, no sistema actual o nivel 6 sería o máis adecuado paira dar ese paso.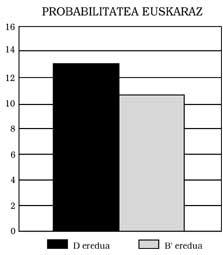
Con todo, coa próxima reforma non sabemos canto ou como van cambiar as cousas, aínda que tede en conta que isto é só una das posibles vías, que a nós nos pareceu máis apropiada, pero cada centro vai marcar o seu camiño. Por que elixir 6º e non calquera outro? Por unha banda, porque o nivel de eúscaro dos alumnos de 6º é bastante rico e, por outro, porque ao distinguir ben o eúscaro dos límites do castelán, non hai interferencias. Como levar a cabo este ensino? Non hai fórmulas máxicas, ou ben dando algúns temas en eúscaro e outros en castelán, ou tratando cada tema en dúas linguas (introdución e repaso nunha lingua e o resto), ou de calquera outra maneira.
Con todo, e nas implicacións pedagóxicas habemos tratado de clarificar, á hora de empezar a traballar as matemáticas na segunda lingua, aspectos como a elaboración dun vocabulario especializado, o tratamento dos problemas, o desenvolvemento da primeira e a segunda lingua, etc. Hai, por tanto, algo elaborado e a que chegar si queremos chegar a ser verdadeiramente bilingües.





