Matemáticas frente a 2ª lengua
Elhuyar: ¿De dónde llegó a este tema?

J. F. L.:
No fue un tema que se había planteado bruscamente; antes de ser profesor de la Universidad impartía clases de matemáticas en una Ikastola del modelo B. Eran alumnos de ciclo superior y el salto a la Enseñanza Media era inmediato. A pesar de que estos alumnos trabajaban las matemáticas en castellano, la intención de los profesores era integrar el mayor número de alumnos en el modelo D de la Enseñanza Media, no era ilógico pensar que podían tener problemas. Esta investigación se inició en la creencia de que era urgente verificar, analizar y clasificar esta previsión.
PaP: ¿Cuáles son los objetivos de este trabajo?
J. F. L.:
Uno de los principales objetivos planteados por nosotros era establecer las bases científicas para replantear la enseñanza de manera que los alumnos del modelo B no tuvieran problemas para trabajar las matemáticas en euskera al incorporarse al modelo D en la Enseñanza Media. Antes, sin embargo, había que analizar si tenían o no problemas, ya que podía haber sido posible que no hubiera ningún problema y que el nuestro fuese una mera sospecha.
El objetivo del modelo B está claro: Capacitar para que cualquier alumno de 8º curso pueda seguir cualquier tema tanto en euskera como en castellano, para lo cual cada centro pondrá los medios necesarios. Según este planteamiento teórico, al pasar a la Enseñanza Media no tendrían inconveniente ni en el castellano ni en el euskera, pero las cosas casi nunca suceden así (y yo me refiero a las matemáticas, que es nuestro tema de estudio), entre otras cosas, porque en algunos centros se trabaja las matemáticas que estudiamos en castellano.

El objetivo principal de esta tesis estaría relacionado con esta preocupación: Es decir, si se cumple o no el objetivo marcado por el modelo B, y cómo afecta al alumnado en caso de incumplimiento.
PaP: ¿Por qué estudiar el binomio matemática/lenguaje?
J. F. L.:
Aunque parezca que las matemáticas y la lengua están distanciadas, en cualquier proceso de enseñanza (incluidas las matemáticas), la influencia de la lengua es innegable. Como dice Sánchez Carrion en su libro Un futuro para nuestro pasado, el profesor está enseñando cualquier tema, pero siempre está trabajando el idioma. Por lo tanto, querer analizar las relaciones entre las matemáticas y la lengua no resulta tan extraño.
En contextos bilingües el problema se agudiza, ya que para ser verdaderamente bilingüe es necesario ser capaz de utilizar ambas lenguas en cualquier tema, incluso en matemáticas. Aquí empieza a surgir problemas reales, ya que esto no se cumple del todo en el modelo B.
El uso de ambas lenguas, por su parte, no debería impedir en ningún caso la asimilación de las diferentes materias, cosa que nadie admitiría. En cualquier programa, sea monolingüe o bilingüe, se establecen unos objetivos mínimos a los que hay que llegar, aunque cada centro tenga libertad para elegir metodología, material, recursos, etc. Si además de conseguirlo llega a dominar la 2ª lengua o la 3ª, mejor.
A pesar de que teóricamente era así, pensábamos que era interesante saber qué pasa realmente y a ello nos pusimos en marcha; analizar si la enseñanza bilingüe supone un obstáculo para la asimilación de los contenidos matemáticos.
PaP: ¿Hasta qué punto el lenguaje puede condicionar el proceso de introducción de las matemáticas?
J. F. L.:
Como se ha mencionado anteriormente, el lenguaje condiciona la enseñanza de cualquier asignatura, y las matemáticas no quedan fuera de esta regla general. Hasta ahora hemos hablado de las matemáticas en su totalidad, pero, siguiendo la taxonomía de Bloom, conviene diferenciar diferentes procesos como el cálculo, la comprensión y la aplicación. En cada una de estas lenguas influye diferente. La importancia del lenguaje simbólico en el cálculo es: 3x4=12 es fácilmente comprensible en cualquier idioma, por supuesto, con unos conocimientos matemáticos mínimos. Sin faltar demasiado, se puede pensar que los del modelo B no tendrán demasiados problemas en este proceso, pero sí en el desarrollo de la comprensión, es decir, en la comprensión de las manifestaciones del profesor o de un texto escrito. En la aplicación, es decir, en la resolución de problemas, cobra especial importancia el lenguaje.
Estos dos últimos procesos serán los que tendremos que analizar especialmente, ya que en ellos influye sobre todo el lenguaje, y en nuestro caso, al hablar de la lengua 2, no de la lengua materna, nos parecía que podía haber problemas.
PaP: ¿Cuál es actualmente el B.O.P.V. ¿y la organización de la enseñanza de las matemáticas en la U.B.I?
J. F. L.:
En la Comunidad Autónoma Vasca se distinguen tres modelos lingüísticos:
- Modelo A, especialmente dirigido a niños erdaldunes. Todo se enseña en castellano y entre otros objetivos mínimos estaría el aprendizaje del euskera; aprender “euskera” y no “euskera”.
- El modelo D, donde todo se hace en euskera, con el castellano como asignatura.
- Por último, nos encontramos con el modelo B que hemos estudiado, en el que el euskera y el castellano son tratados teóricamente al menos al mismo nivel, pero trabajan las matemáticas, la escritura y la lectura en castellano, mientras que el resto de asignaturas se imparten en euskera. ¿Por qué ocurre así? En algunas teorías y estudios se ha demostrado que para que no haya retrasos en estos temas importantes es necesario tomar los conceptos básicos en la lengua materna.
Si bien en el B.O.U. se diferencian estos tres modelos, no ocurre lo mismo en la Enseñanza Media, ya que aquí sólo hay dos modelos, los modelos A y D. En teoría, los alumnos del modelo B. Una vez terminada, ya estarían preparadas tanto para el modelo A como para el modelo D.
¿Es capaz el alumno de empezar a trabajar las matemáticas en castellano hasta el 8º curso? ¿No va a explicar retraso respecto a los que han aprendido euskera?
PaP: Pero cuando se da ese paso, ¿qué es lo que más inconveniente supone: los cambios lingüísticos o las dificultades del tema?
J. F. L.:
Ambos tienen importancia y ambos van unidos. Cualquiera podría pensar que no sería más que una falta de costumbre, una falta de costumbre que se superaría tras unos meses mal. En parte es así, pero no sólo eso.
En la Enseñanza Media los conceptos y contenidos se complican exigiendo un mayor desarrollo lingüístico. Los modelos D o A también pueden tener este problema, pero el desfase que pueden tener los demás es más grave. Creemos que aunque a la hora de analizar las conclusiones vamos a concretar más, el cambio lingüístico debería hacerse antes de pasar a la RCP.
PaP: ¿Cómo habéis planteado el estudio empírico?
J. F. L.:
Hasta ahora he tratado de dar cuenta del planteamiento teórico, pero este trabajo no ha sido una mera teorización. A la hora de diseñar el estudio nos pareció que teníamos que hacer cuatro grupos diferentes de 8º curso:
Grupo formado por un número de alumnos del modelo A (grupo A) con alumnos del modelo B, dos grupos (grupo B y grupo B) otro grupo del modelo D (grupo D)
A y B pasamos las pruebas en castellano y a D y B’ en euskera. Dado que nuestro estudio estaba dirigido al modelo B, aquí teníamos la oportunidad de compararlo con dos grupos en euskera y castellano: Grupo B con A y B’ con D.
Para completar la muestra, acudimos a los colegios públicos y a las ikastolas de la Comunidad Autónoma Vasca con el objetivo de conseguir unos 900 alumnos. No fuimos a los centros privados, entre otras cosas porque en Álava no encontramos al menos D.
Las variables consideradas serían, por un lado, la propia matemática como variable dependiente (distinguiendo el cálculo a abordar dentro de las matemáticas, la comprensión de una explicación, la comprensión y aplicación del texto escrito) y, por otro, el nivel de euskera que hemos considerado como variables independientes, el tipo de centro, el modelo lingüístico, el nivel socioeconómico, la edad, el sexo, etc.
PaP: ¿Cómo habéis medido el nivel de matemáticas?
J. F. L.:
Hemos utilizado tres pruebas diferentes para medir conocimientos matemáticos:- Test extranjero EIA ( International Evaluation Achievement ) de Estados Unidos. Partiendo de la versión en castellano, antes de pasar a los alumnos, teníamos que traducir, validar y controlar la fiabilidad. Este fue el primer paso. Esta prueba consta de 40 ítems que recogen contenidos del nivel 8: geometría, fracciones, aritmética,... Con esta prueba se miden cuatro procesos diferentes: cálculo, comprensión, aplicación y análisis (los relativos al análisis son sólo dos ítems y al no tener influencia significativa en la investigación apenas se han tenido en cuenta).
- Para poder medir la comprensión de la exposición del profesor, un profesor de la RCP, tras pasar una explicación previamente grabada en vídeo, les preguntamos sobre ella. La duración del vídeo es de hora y media y, por supuesto, ha tenido dos versiones, una en euskera y otra en castellano.
- Para medir la comprensión del texto escrito, se seleccionó el tema de la probabilidad del libro BBB-1 publicado por Elhuyar. No completa, es demasiado larga. Dado que el texto se encontraba en euskera, se tradujo al castellano para pasar a los grupos A y B. Tras leer el texto había que responder a varias preguntas, unas en euskera y otras en castellano.
Tanto a la hora de elegir la prueba de probabilidad como a la hora de elegir la de vídeo, nos han limitado dos condiciones principales: por un lado, el hecho de que el tema sea nuevo, ya que de ser tratado previamente los resultados serían “no reales”, y por otro lado, el hecho de que sea un tema a nivel de desarrollo del alumnado.
Para medir variables independientes, hemos tenido que crear algunas pruebas, pero no todas, como el test estandarizado D-48 que hemos utilizado para medir la inteligencia. La prueba que hemos creado es la adaptación al cuento Peru makur. En esta prueba en la que tras la lectura del cuento aparecen las preguntas que le corresponden, se medirá su nivel de lectura en euskera. Se miden principalmente tres aspectos: velocidad de lectura, porcentaje de comprensión y porcentaje de velocidad de lectura.
La nueva herramienta supone la realización de un trabajo “extra” previo a su incorporación a la investigación real, como la realización de la misma prueba y el control de fiabilidad y utilidad. Una vez hecho esto, estaría dispuesto a pasarlo.
PaP: ¿Las herramientas de medición utilizadas por vosotros son utilizables por cualquier profesor?
J. F. L.:
En general sí, aunque algunas pruebas han sido especialmente preparadas para esta investigación (Vídeo prueba, texto utilizado para medir probabilidades y prueba basada en el cuento Peru makur). El resto, sin embargo, es accesible para cualquier persona, siempre y cuando el nivel de los alumnos sea 8 o superior (test EIA, test D-48 y cuento Peru makur).
PaP: ¿Cuál sería la conclusión más destacable?
J. F. L.:
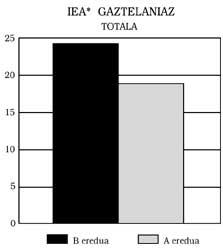
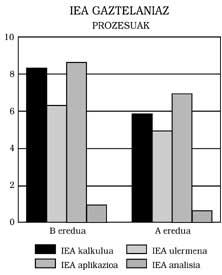
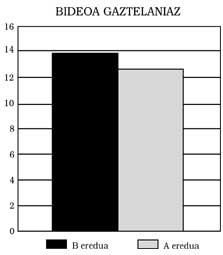
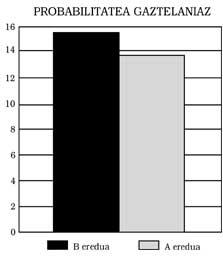
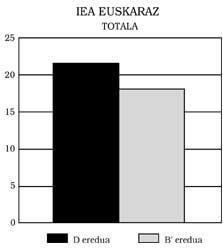
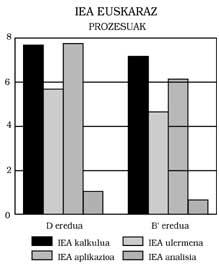
Se pueden extraer tres conclusiones principales: 1) Los alumnos del modelo B presentan al responder en castellano un nivel mínimo equivalente al de los del modelo A. Esto significa: Los del modelo B no muestran ningún retraso matemático, aunque el modelo de enseñanza sea bilingüe. Más aún, como se puede observar en las Figuras 1, 2, 3 y 4, han obtenido mejores puntuaciones que las del modelo A. En algunos casos, además, las diferencias han sido estadísticamente significativas, pese al control de la inteligencia y del nivel socioeconómico. Cualquiera podría pensar que la mejor puntuación es la promovida por el efecto beneficioso del bilingüismo, pero no nos hemos atrevido a decirlo. Una investigación más profunda, que no ha sido una de nuestras metas.
La razón real de esta diferencia entre los modelos A y B, tal y como hemos analizado, estaría en el tipo de centro. Mientras en el modelo B se encuentran las ikastolas y los centros públicos, en el modelo A sólo los centros públicos (en las ikastolas no hay modelo A). Por otra parte, el contexto en el que se ubican los centros públicos del modelo A suele ser marginal, en el que se presentan abundantes y frecuentes problemas de integración, adaptación, etc.
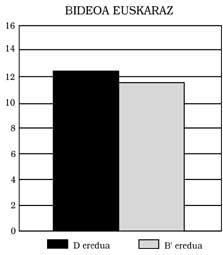
Esta puede ser la razón principal de esta diferencia. 2) Comparando los del modelo B’y D, en todas las pruebas se han mostrado los del D por encima (ver figuras 5, 6, 7 y 8 para ello). Estas diferencias son significativas en aspectos como la aplicación y la explicación de un profesor o la comprensión de un texto, pero en otros como el cálculo no ocurre. ¿Cuál es su explicación? Al tener un mayor nivel lingüístico, en aquellos casos en los que la influencia de la lengua es elevada, los del modelo D obtienen mejores resultados. 3) La tercera conclusión es que se han contrastado los resultados obtenidos en otros contextos bilingües, es decir, que cuanto más se ha trabajado y utilizado la segunda lengua en la escuela, mayor es el grado de competencia, sin que la primera lengua sufra ningún retraso.
¿Qué ha pasado en nuestro caso? Hemos observado diferencias significativas entre los modelos B. En cualquier caso, cuando hablamos del modelo B, hay que decir que se trata de un modelo muy generalizado, ya que se pueden encontrar modelos B más euskaldunes y castellanoparlantes. Esta clasificación se realiza en función de tres variables: porcentaje de euskaldunes entre profesorado, porcentaje de asignaturas del ciclo superior que se cursan en euskera, y por último, a partir del curso 6, trabajar las matemáticas en euskera o en castellano.
La diferencia entre los modelos B es real, ya que en las pruebas matemáticas el modelo B más euskaldun obtiene una mejor puntuación. Al pasar la prueba en castellano apenas ha habido diferencias. En definitiva, lo que se consigue con la lengua en algunos contextos bilingües, lo hemos conseguido con la matemática, es decir, cuanto más trabajemos las matemáticas en la segunda lengua, más competencia es en la segunda lengua sin retrasos en la lengua materna.
La verdad es que estos resultados no han hecho creer demasiados imprevistos en nosotros, tal vez la mayor de las imprevistos haya sido la diferencia entre los modelos B y A, que esperábamos resultados inversos. Hemos dicho, sin embargo, cuál puede ser su razón.
PaP: ¿Cómo reestructuraríais la enseñanza ante estas conclusiones para que los resultados sean ‘óptimos’?
J. F. L.:
De acuerdo con lo visto, en primer lugar se modificaría la estructuración de las matemáticas en el modelo B, al menos en lo que se refiere al uso de la lengua (si se quiere alcanzar el objetivo principal al que se ha hecho referencia, que una vez finalizado el nivel 8, sea capaz de cursar sus estudios tanto en euskera como en castellano). Para ello es necesario que a partir de cierto nivel se comience a trabajar también las matemáticas en euskera, y como decimos en las implicaciones pedagógicas de la tesis, en el sistema actual el nivel 6 sería el más adecuado para dar ese paso.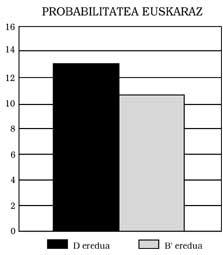
Sin embargo, con la próxima reforma no sabemos cuánto o cómo van a cambiar las cosas, aunque tened en cuenta que esto es sólo una de las posibles vías, que a nosotros nos ha parecido más apropiada, pero cada centro va a marcar su camino. ¿Por qué elegir 6º y no cualquier otro? Por un lado, porque el nivel de euskera de los alumnos de 6º es bastante rico y, por otro, porque al distinguir bien el euskera de los límites del castellano, no hay interferencias. ¿Cómo llevar a cabo esta enseñanza? No hay fórmulas mágicas, o bien dando algunos temas en euskera y otros en castellano, o tratando cada tema en dos lenguas (introducción y repaso en una lengua y el resto), o de cualquier otra manera.
Sin embargo, y en las implicaciones pedagógicas hemos tratado de clarificar, a la hora de empezar a trabajar las matemáticas en la segunda lengua, aspectos como la elaboración de un vocabulario especializado, el tratamiento de los problemas, el desarrollo de la primera y la segunda lengua, etc. Hay, por tanto, algo elaborado y a qué llegar si queremos llegar a ser verdaderamente bilingües.





