Quantum gravitation. Supergravitational theories
Introduction Introduction Introduction Introduction

The success obtained by quantum electrodynamics pushes scientists to unify the electromagnetic field and the weak, for which it is necessary to devise a more powerful gauge symmetry. This new symmetry is based on the isotope symmetry of spin and the sudden rupture of symmetry. This electroweak theory was confirmed experimentally in 1983.
In this sense, it is trying to theorize a more powerful gauge zone in order to join violent forces. The BHT theories have been created (1). These theories have not yet been confirmed experimentally. But theoretical physics cannot wait and has begun to theorize another wider field to unify the gravitational with previous forces. The goal of quantum gravitation is to achieve this superbroad theory.
1.- Universe of bosons and fermions
The Theories of Greater Unity (TMH) group three areas of the physical world, but not the fourth, gravitation. Gravity has a great resistance to join with other forces.
In this context, two problems arise. On the one hand we do not know the symmetry necessary to unite the four forces. On the other hand, we still do not have a gravitational theory that can be compactadora of quantum mechanics, since when one wants to define gravitation through the exchange of gravitons (those of the gravitational field), they appear infinite eliminating the theory.
But we know what can be done to make those infinites disappear: Create a symmetry more powerful than the one that has so far any theory. And that was precisely the path chosen by theoretical physics. In 1970 physicists promulgated the first supergravitational theories. The symmetry used in these theories is so powerful that it adds all the forces existing in nature. That is why these theories are called supersymmetric.
Supergravitation is a generalization of Einstein's theory of relativity. Supergravitation describes gravitational phenomena at quantum level.
Supergravitation is a supersymmetric formulation of gravitation. This supersymmetry was formulated at the beginning of 70 by three independent paths. These investigations were carried out in the United States, the Soviet Union and Europe.
The essence of these studies is this. All fractions in the universe can be divided into two groups in terms of their spin: The two groups are bosons and fermions. The bosons are particles containing no spin or simply spin. No fermions: these have spin fractions. This, despite being very hard for our mind, means that these particles have a double rotation.
The behavior of this type of distributed fractions is very curious. Fermons do not want to be related to other particles of their family. This behavior is defined by the principle of exclusion of Pauli. According to this principle, two fermios cannot divide between themselves a same quantum number.
Faced with this selfish behavior, we have bosons. These do not put obstacles to working with each other and are grouped into groups up to one level, multiplying their effects, which can be detected macroscopically through our measuring tools.
As a consequence of this behavior, the worlds of fermions and bosons have been considered in the scientific world as a constant fusion. For this reason, these supergravitational theories were taken with exclamation, since their foundations were in the union of bosons and fermions.
2.- Supersymmetry
Mathematically, a supersymmetry operation is the realization of two roots of Lorentz/Poincaré symmetry. Physically equivalent is to turn the fermium into a boson (or vice versa).The supersymmetric theory is based on numerical elements that do not present a commutative characteristic. The reason for entering these numbers is related to the principle of exclusion of Pauli. This principle prohibits the coexistence of two fermions at one point.
The origin of supergravity is based on a surprising knowledge of supersymmetry. The transfomation of the fermions boson, that is, a particle moves from one point to another throughout space time. If the displacement of this particle is obtained through a supersymmetric transformation, it suggests a deep relationship between supersymmetry and spatial structure.
If in addition the repetition of the transformation of the supersymmetry is the transformation of Poincaré and it is taken into account that the reduced invariance of Poincaré is the symmetry that produces general relativity, hence it is deduced that there is a very narrow connection between supersymmetry and gravitation. Hence, theoretical physicists have begun to study supersymmetric theories.

Gauge is the basis of supersymmetric theory, as mentioned above, the space-time displacement of the two supersymmetric rotations. Physically it can be interpreted as: The repetition of the transformation of a supersymmetry causes the displacement of a physical fraction.
To achieve a reduced supersymmetric theory, we must add to each symmetry (rotation) a snake field. Meanwhile, displacement in space time is the transformation of Poincaré. This transformation makes graviton to be considered as an adequate gauge particle. Thus, without further ado, the supersymmetric theory is transformed into a supergravitational theory.
If it is supergravity, it gives us a description of the general relativity, being its quantum language. This theory predicts the existence of spin particles 3/2. The experimental observation of these particles would give a great boost to supergravitation.
3.- General theories of supergravitation
The above mentioned supergravity has been generalized in the set of unified theory, known as the general theory of Supergravitation.
In this group we have 8 theories. Among them, N=1 (2), gravitation in its original form. And the most powerful is N=8. In this model, a family of very abundant fractions is defined. In this family we have 70 particles. Among these particles are all those that are known today and many others that must be found. Such a model brings together all the fields of physics. Put another way, this theory would be a single entity that controls all of Nature. In this context, for the first time in the history of science, matter and force would appear in a single description.
The greatest achievement of this set of teoris is the degree of symmetry that is achieved in them. When the supersymmetry joins the inner symmetry, all the fractions that graviton creates are added. And this is very important because all diagrams can be defined according to the gravitational diagram. And the sum of all these diagrams (to calculate the probability of interactions) is finite. Therefore, these theories are renormalizable.
The renormalization, the deep symmetry, the unity of fields,... are the objectives that have reached the supergravitational theories. Physicists (theoretical physicists) enjoy enormous confidence in these theories. There are those who say that theory N=8 is the summit of theoretical physics.
To date, physical theories have been taken as models of interpretation of reality. As these models improved, the integration between theory and rality was adapted. Some scientists of today have dared to explain the following opinion:
"The supergravitational theory N=8 has an enormous mathematical adequacy with reality, since this is no longer the model of reality, but reality."
4.- Quantization of spatial continuity
The most terrible and dark part of quantum gravitation is the influence that quantization can have on the spatial framework.
As mentioned above, in order to obtain unified theory, gravitation and quantum mechanics must be compacters. In other words, the gravitational field must be quantified. However, according to the general theory of relativity, the gravitational field is nothing more than a deformation of the continuous space.
At this point an important node is created, since if gravity is quantified, the very framework of physical phenomena (space-time continuous) becomes quantum object. And the latter will have enormous physical-philosophical implications.
In the conventional quantum theory of the fields, the spatial substrate was stable. In the theory of quantum gravitation, this support (substrate) will not only influence quantum fluctuations that occur within it, but will also be fluctuating.
From this point of view, if we analyze the behavior of the spatial framework at the microcosm level, three different levels will appear to us.
On the first level we find the nucleus of the atom at a spatial height of about 10 -12 cm (far superior to the length of the Planck). At this level, quantum fluctuations of the gravitational field are very small and the geometry of the substrate can be considered continuous.
If the distance level falls and we reach 10 -30 cm (wavelength around the Planck), we dive into the BHT scale (3). At this level important fluctuations in substrate geometry begin to appear and now appears wrinkled what was formerly a flat topology.
If we continue descending on the distance scale, we will reach the length of Planck (10-30 cm), the smallest distance with physical meaning. Here the spatial continuity fluctuates with force, as if in the storm we were among the waves of the sea. This space time is quantified and its causal structure is fluctuating and indefinite.

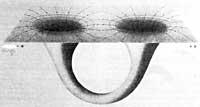
On the scale of the Planck field it is not possible to distinguish between past and future. At such small distances, processes that are not allowed in non-quantum relativity, such as the existence of speeds higher than the speed of light, can probably occur.
5.- Variable topology
In this context arises the concept of changing topology invented by Wheeler. The extrapolation of fragile zones to the areas of the Planck, according to this conception, can make the fluctuations of the geometry very aggressive in the same space time generating black holes. In this situation, the topology of the substrate would be very altered. In this context, violence and imbalance would be kings. The temporary space structures of the support would be very complex, creative and missing.
According to Wheeler's theory, the excitement of this aggressive space sea would reveal itself through elementary particles. And the different nature between particles is given by the topology attached to each excitation. According to Wheeler, to know the behaviors of the trunk fractions, we should first understand the nature of the state of quantum gravitation. In the elementary particle, phenomenology would be reduced to the chemistry of geometry.
What is the mathematical model that can be used to describe this quantum chaos?. How to describe topological transitions that occur in this framework?
Some models have already been proposed (4), but in scientific environments a complete consensus has not been reached. Some scientists have proposed to consider spatial geometry as a secondary reality. This reality would only have relevance in the distances of Planck. But this explanation poses another problem: What is the new character of reality if in quantum gravitation the spatial substratum must be replaced?
The answer to this question is being shaped by two different aspects. The first difference is the supergravity, with its powerful symmetries. On the other hand, it is the review of the multidimensional worlds created by Kaluza and Klein sixty years ago, but reinterpreted now from the perspective of quantum perspective. These multidimensional universes will be the ones we will analyze in the next chapter.
OBSERVATIONS
- BHT: Theories of the Batsunik Handiena GUT: Grand Unified Theories GTU: Large Unified Theories n is the number of gravity with spin 3/2 of each theory. In this quark scale and leptoie lose identity and join electromagnetic, weak and violent forces. Recently, S.W. Hawking presents a mathematical model to describe spatial topology. In 1984 a close calculation is presented for the transformation of this topology. See A. Strominger in bibliography.
BIBLIOGRAPHY BIBLIOGRAPHY
- DAVIES, Paul: The edge of Infinity ; J.M. Dent and Sons Ltd. London, 1985.
- DE WIT Bryce: Relative gravity ; Scientific American, Feb, 1984
- J.M. DUFF ISHAM C.J. : Quantum Structure of Space and Time ; University Press, Cambridge, 1982.
- STROMINGER, A.: Phys. Rev. Lett. , 52, 1733; (1984).
- WEINBER, S: Unified theories of interactions between elementary particles ; Scientific American, July, 1974.






