Astronomía XVII. século

A teoría do movemento dos planetas tivo agora un desenvolvemento enorme. Estamos no ano 1600. Tanto o Renacemento como a Reforma están a pasar. No campo da astronomía, algúns utilizaban as vantaxes de cálculo que ofrecía o sistema de Copérnico, pero sen aceptar as súas consecuencias tanto físicas como filosóficas. Neste silencio escoitouse una soa voz que expresaba o conflito que viña. Giordano Bruno (panteísta antiortodoxo e transeuropeo) dicía que os límites do Universo estaban moi lonxe (é dicir, no infinito) e que o noso Sistema Solar é só un sistema entre outros infinitos. Por todas as herejías mencionadas, a Inquisición xulgouna e queimou en 1600.
Con todo, as sementes dunha nova ciencia estaban germinando en calquera lugar. En Inglaterra Francis Bacon (1561-1626) e William Gilbert (1540-1603); en Italia Galileo Galilei (1564-1642); en Copenhague Tycho Brahe (1546-1601). É o primeiro home que desde a época grega realizou melloras nas observacións astronómicas. Case toda a súa vida, cunha precisión que até entón non era a mesma, pasou a observar os movementos dos planetas. Os seus datos eran, en moitas ocasións, vinte veces máis precisos que os de Copérnico, e todo iso sen inventar o telescopio.
Tras a morte de Tycho Brahe, o alemán Johannes Kepler (1571-1630) deulle a continuación, por unha banda facendo outras observacións e por outro realizando una exhaustiva investigación de todos os datos tomados. Mentres Tycho desenvolveu no seu día un sistema planetario especial, Kepler estaba a favor de Copérnic. O obxectivo dos seus traballos era facer máis exactos que as táboas astronómicas dos movementos dos planetas naquel período. Pero non quería máis que adaptar a teoría heliocéntrica na base, porque pola súa harmonía e sinxeleza, víaa fascinada e a gusto. Desde o inicio das súas obras, a metafísica pitagórica e a neoplatónica tiveron una gran influencia. Esta tendencia seguiu durante o Renacemento desafiando a hexemonía aristotélica.
Segundo Kepler, a tendencia da intelixencia divina era dalgunha maneira xeométrica e as características desta orde podían atoparse nas relacións matemáticas que conducían o sistema heliocéntrico. Por iso, nunha das súas primeiras obras trataba de relacionar os seis planetas que se coñecían e as súas distancias ao Sol co cinco sólidos regulares da xeometría.
Cando quería adaptar os novos datos obtidos da órbita de Martitz ao sistema de Copérnic e tras catro anos de traballo duro, chegou a unha conclusión moi importante, que era imposible! Os novos datos situaban a órbita a oito minutos do esquema de Copérnico. Aínda que Copérnic no seu día, sabendo que os datos utilizados non eran exactos, non deu importancia a esta diferenza, Kepler sabía que os datos de Tycho eran moito máis exactos que a diferenza mencionada, polo que o conseguido era inaceptable. Por iso, e coa honestidade que corresponde aos científicos, non se tentou negar as observacións e inventar novas hipóteses paira salvar a teoría aceptada por eles mesmos. Con todo, paira el eses oito minutos indicaban: Que o sistema de Copérnic non era capaz de expresar o movemento real de Marte. Así que abandonou o sistema de Copérnico coas súas esferas concéntricas e epiciclos.
Paira Kepler iso sería moi duro, porque el era partidario do sistema de Copérnic. Con todo, seguiu adiante e paira iso tivo que romper o xugo que unía o sistema de Copérnico coa antiga Grecia. Cando estudaba as traxectorias dos planetas segundo a teoría heliocéntrica, ocorréuselle que a imaxe dos percorridos podía ser da elipse (características da elipse a. C.). II. Eran coñecidos desde o século XIX). Se se aceptaba isto, é dicir, que o percorrido natural dun planeta é elipse, construíase un esquema xeométrico de gran facilidade paira o mundo. Neste esquema, todos os planetas móvense en órbitas elípticas, co Sol nun foco. Esta lei é una das tres leis principais de Kepler e xeralmente dise que é a primeira.
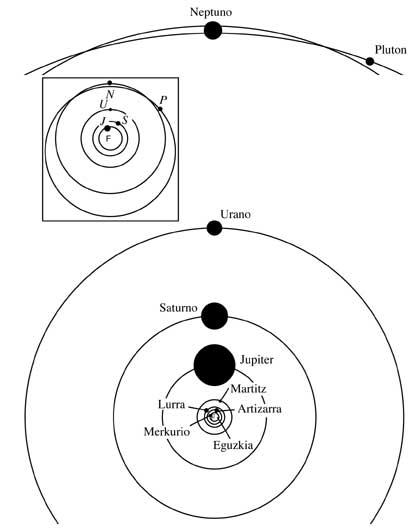
Esta primeira lei de Kepler, ao dirixir a teoría heliocéntrica de Copérnic, dános una imaxe moi sinxela do sistema solar. Todos os epiciclos e excéntricos de Copérnic descártanse: as órbitas son só elipses. Na imaxe pódese ver o esquema actual e simple do sistema solar
Estas elipses son case círculos e todas as órbitas atópanse case no mesmo plano, fóra de Plutón. Isto ten una forte inclinación e tanto na imaxe como noutras, as órbitas de Neptuno e Plutón non se humillan en ningún punto do espazo.
Probablemente Kepler foi feliz ao chegar a unha conclusión tan sinxela como esta (tras prescindir dos epiciclos e excéntricos que eran moi complicados), vendo que todo se cumpría ben a través das elipses. Con todo, en si mesma tiña una preocupación: nós podemos entender a tendencia de Platón a recoñecer que os movementos circulares e uniformes eran naturais, pero por que a Natureza elixe a elipse? Paira responder correctamente a esta pregunta hai que esperar á chegada de Newton, que nos dixo que a lei da elipse é una consecuencia doutra lei da Natureza moito máis ampla. Por tanto, deixemos o tema por agora.
Por iso, debemos pensar que a primeira lei de Kepler é un resumo das observacións realizadas, é dicir, una lei empírica. Pero, aínda que esta lei dános conta de todas as localizacións dun planeta, non nos di nada acerca de cando será ese planeta nun ou outro lugar, é dicir, indícanos a imaxe da órbita, pero a súa velocidade non. Por tanto, esta lei queda moi curta porque os astrónomos (e Kepler tamén) queren saber de antemán cando será un planeta nun punto. Por iso, antes de que salga a súa primeira lei, Kepler tiña establecida una segunda lei que nos indica os cambios na velocidade dun planeta.

Kepler sabía que se existise una relación matemática entre a velocidade dunha e outra posición da órbita dun planeta, o sistema sería moito máis sinxelo. Se se descubrise esta relación, o movemento dun planeta podíase expresar con moi poucos datos. Necesitábanse dous datos paira proporcionar a mesma elipse, o terceiro paira alcanzar a velocidade nun punto concreto do percorrido (no perihelio, por exemplo, o punto máis próximo ao Sol) e outro paira coñecer a inclinación do plano orbital respecto doutros planetas. Pero ninguén coñecía esa relación. Por iso, cando se lle ocorreu esta lei dise que estaba na éxtase, pero o que sabemos é que paira atopala tivo que analizar unha chea de datos e realizar un traballo constante e duro.
En calquera caso, o camiño que seguiu paira conseguir esta segunda lei é sorprendente, xa que en base ás tres erróneas hipóteses chegou á súa conclusión. En palabras de Kepler, a órbita que describen os planetas débese á forza que exerce o Sol e cuxo valor era inversamente proporcional á distancia entre o Sol e o planeta. A velocidade e a forza que impulsa o planeta eran directamente proporcionais entre si e, por tanto, inversamente proporcionais á distancia. Esta hipótese (é dicir, que a velocidade sexa proporcional á forza) é hoxe inaceptable, pero se pode ver como a idea de Aristóteles ou como algo que o sentido común daba naquela época.
Segundo esta hipótese, o tempo que tarda un planeta en percorrer una pequena distancia durante o percorrido sería proporcional á distancia ao Sol. Isto é case totalmente correcto e así nalgúns puntos da órbita. Por tanto, Kepler quería calcular o tempo necesario paira completar un gran tramo de percorrido (e por tanto cando a distancia ao Sol é variable). Paira iso, tivo en conta as distancias de todos os pequenos arcos que forman este gran tramo e concluíu que ese tempo é directamente proporcional á superficie que cobre a liña que vai desde o Sol até o planeta. Segundo esta segunda lei, a Terra (ou si quérese o Sol no fondo das estrelas) enténdese que no inverno se move máis rápido que no verán, algo que tanto Kepler como os seus predecesores coñecían perfectamente.
Ambas as leis foron publicadas en 1609 no libro Astronomía Nova. Pero Kepler non gustaba e tiña una preocupación: non se coñecía ningunha relación entre os movementos dos diferentes planetas. Cada planeta movíase no seu elipse e á súa velocidade, pero parece que non había un modelo xeral paira todos. Kepler pensaba que debía existir este modelo xeral, polo que debía existir una relación que relacione todos os movementos presentes no sistema solar. Kepler partiu tras esta relación e paira iso utilizou a teoría musical, segundo os seguidores de Pitágoras, en busca dun vínculo entre as órbitas dos planetas e as notas musicais. Se a súa prolífica obra chamouse A harmonía do mundo, quería expresar algo.
Crer nesa relación (ou mellor devandito, a súa obsesión) pode, por unha banda, expresar a primeira fe máxica dos números que tiña Kepler, pero tamén a tendencia de todos os xenios da ciencia. Segundo eles, a Natureza é uniforme e sinxela. Esta crenza deu una gran axuda aos científicos e una forza paira superar os obstáculos. Ese é o caso de Kepler, que tras descubrir a súa terceira lei por sufrir mil desgrazas persoais, foi capaz de escribir:

... despois de atopar durante moito tempo una distancia real das órbitas utilizando os datos de Brahe, una relación real... o feito de que exista un consenso tan amplo entre o traballo que presento hoxe en día e o traballo que eu realicei durante dezasete anos sobre as observacións de Brahe, limpou as miñas sombras da miña mente e pensaba que ao principio estaba nos meus soños...
Segundo a linguaxe actual desta lei, se o período dun planeta é T (é dicir, o tempo de dar una volta completa ao redor do Sol) e R o seu radio medio, T 2 = K . R é 3, sendo K una constante igual paira todos os planetas. No caso da Terra T = 1 ano e R = 15 x 10 7 km, polo que se coñecemos o seu radio R paira calquera outro planeta, podemos atopar o período.
Esta terceira lei chámase lei harmónica, porque representa una bonita relación harmónica entre os planetas.
A través de todo iso, relacionando loxicamente o noso sistema solar, vémolo como un todo simple: a nosa intelixencia capta o universo de Kepler cunha mirada e é capaz de expresar matematicamente as leis que o rexen.
Kepler, a partir dos datos de Brahe, tentou construír táboas detalladas de movementos planetarios. Paira levar a cabo este labor tivo que abandonar algunhas das opinións aceptadas naquela época. Esta actitude era completamente nova, é dicir, dar prioridade ás observacións, se estas realizábanse de forma precisa e cuantitativa. Outro aspecto a destacar é a predición do uso da linguaxe matemática na expresión de leis físicas. Posteriormente, as ecuacións serían as expresións naturais das leis físicas.
Por outra banda, o movemento dos planetas na súa órbita no sistema de Kepler non se consideraba producido por ningún deus (como o demostraban os escolásticos), nin polas súas formas esféricas representaban movementos circulares. No seu último libro ( Mysterium Cosmographicum ) cóntanos como cambiou as súas opinións en 1596:

Nunha época cría firmemente que a forza do movemento dun planeta estaba nunha alma... Con todo, cando pensei que esta causa do movemento diminuía coa distancia (é dicir, como a luz do Sol diminúe coa distancia a este astro), cheguei á conclusión de que esa forza debía ser substancial, non literalmente, senón… como dicimos que a luz é algo substancial, é dicir, algo non espiritual e que salgue dun corpo substancial.
En 1605 escribe a un amigo:
Ocupeime moito da investigación de causas físicas. O meu ensaio consistiu en demostrar que a máquina celeste debe compararse cun organismo divino e non cunha obra de reloxaría (e quen cre que un reloxo ten alma, atribúe a honra ao relojero), e que nese reloxo todos os movementos diferentes son o resultado dunha simple forza magnética, como todos os movementos da máquina dun reloxo son consecuencia dun único peso. Ademais, demostro que esta concepción física debe expresarse mediante cálculo e xeometría.
En Kepler podemos ver claramente o cambio iniciado en Europa dous séculos antes. A observación día a día, os resultados, en definitiva, deixan paso ás simples especulacións e as teorías teñen que basearse nesa realidade. Por iso podemos dicir que Kepler fixo una primeira reivindicación da actitude moderna da ciencia.





