Astronomía XVII. siglo

La teoría del movimiento de los planetas ha tenido ahora un desarrollo enorme. Estamos en el año 1600. Tanto el Renacimiento como la Reforma están pasando. En el campo de la astronomía, algunos utilizaban las ventajas de cálculo que ofrecía el sistema de Copérnico, pero sin aceptar sus consecuencias tanto físicas como filosóficas. En este silencio se escuchó una sola voz que expresaba el conflicto que venía. Giordano Bruno (panteísta antiortodoxo y transeuropeo) decía que los límites del Universo estaban muy lejos (es decir, en el infinito) y que nuestro Sistema Solar es sólo un sistema entre otros infinitos. Por todas las herejías mencionadas, la Inquisición la juzgó y quemó en 1600.
Sin embargo, las semillas de una nueva ciencia estaban germinando en cualquier lugar. En Inglaterra Francis Bacon (1561-1626) y William Gilbert (1540-1603); en Italia Galileo Galilei (1564-1642); en Copenhague Tycho Brahe (1546-1601). Es el primer hombre que desde la época griega realizó mejoras en las observaciones astronómicas. Casi toda su vida, con una precisión que hasta entonces no era la misma, pasó a observar los movimientos de los planetas. Sus datos eran, en muchas ocasiones, veinte veces más precisos que los de Copérnico, y todo ello sin inventar el telescopio.
Tras la muerte de Tycho Brahe, el alemán Johannes Kepler (1571-1630) le dio la continuación, por un lado haciendo otras observaciones y por otro realizando una exhaustiva investigación de todos los datos tomados. Mientras Tycho desarrolló en su día un sistema planetario especial, Kepler estaba a favor de Copérnic. El objetivo de sus trabajos era hacer más exactos que las tablas astronómicas de los movimientos de los planetas en aquel período. Pero no quería más que adaptar la teoría heliocéntrica en la base, porque por su armonía y sencillez, la veía fascinada y a gusto. Desde el inicio de sus obras, la metafísica pitagórica y la neoplatónica tuvieron una gran influencia. Esta tendencia siguió durante el Renacimiento desafiando la hegemonía aristotélica.
Según Kepler, la tendencia de la inteligencia divina era de alguna manera geométrica y las características de este orden podían encontrarse en las relaciones matemáticas que conducían el sistema heliocéntrico. Por ello, en una de sus primeras obras trataba de relacionar los seis planetas que se conocían y sus distancias al Sol con los cinco sólidos regulares de la geometría.
Cuando quería adaptar los nuevos datos obtenidos de la órbita de Martitz al sistema de Copérnic y tras cuatro años de trabajo duro, llegó a una conclusión muy importante, ¡que era imposible! Los nuevos datos situaban la órbita a ocho minutos del esquema de Copérnico. Aunque Copérnic en su día, sabiendo que los datos utilizados no eran exactos, no dio importancia a esta diferencia, Kepler sabía que los datos de Tycho eran mucho más exactos que la diferencia mencionada, por lo que lo conseguido era inaceptable. Por ello, y con la honestidad que corresponde a los científicos, no se intentó negar las observaciones y inventar nuevas hipótesis para salvar la teoría aceptada por ellos mismos. Sin embargo, para él esos ocho minutos indicaban: Que el sistema de Copérnic no era capaz de expresar el movimiento real de Marte. Así que abandonó el sistema de Copérnico con sus esferas concéntricas y epiciclos.
Para Kepler eso sería muy duro, porque él era partidario del sistema de Copérnic. Sin embargo, siguió adelante y para ello tuvo que romper el yugo que unía el sistema de Copérnico con la antigua Grecia. Cuando estudiaba las trayectorias de los planetas según la teoría heliocéntrica, se le ocurrió que la imagen de los recorridos podía ser de la elipse (características de la elipse a. C.). II. Eran conocidos desde el siglo XIX). Si se aceptaba esto, es decir, que el recorrido natural de un planeta es elipse, se construía un esquema geométrico de gran facilidad para el mundo. En este esquema, todos los planetas se mueven en órbitas elípticas, con el Sol en un foco. Esta ley es una de las tres leyes principales de Kepler y generalmente se dice que es la primera.
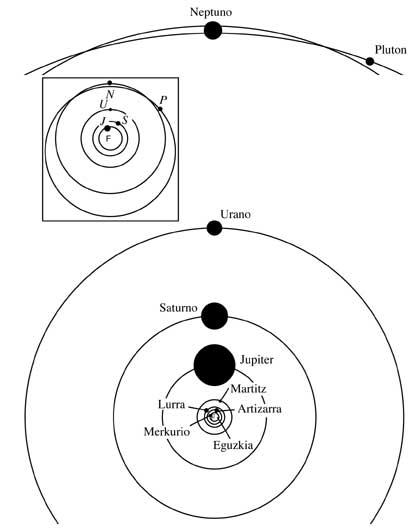
Esta primera ley de Kepler, al dirigir la teoría heliocéntrica de Copérnic, nos da una imagen muy sencilla del sistema solar. Todos los epiciclos y excéntricos de Copérnic se descartan: las órbitas son sólo elipses. En la imagen se puede ver el esquema actual y simple del sistema solar
Estas elipses son casi círculos y todas las órbitas se encuentran casi en el mismo plano, a excepción de Plutón. Esto tiene una fuerte inclinación y tanto en la imagen como en otras, las órbitas de Neptuno y Plutón no se humillan en ningún punto del espacio.
Probablemente Kepler fue feliz al llegar a una conclusión tan sencilla como esta (tras prescindir de los epiciclos y excéntricos que eran muy complicados), viendo que todo se cumplía bien a través de las elipses. Sin embargo, en sí misma tenía una preocupación: nosotros podemos entender la tendencia de Platón a reconocer que los movimientos circulares y uniformes eran naturales, pero ¿por qué la Naturaleza elige la elipse? Para responder correctamente a esta pregunta hay que esperar a la llegada de Newton, que nos dijo que la ley de la elipse es una consecuencia de otra ley de la Naturaleza mucho más amplia. Por lo tanto, dejemos el tema por ahora.
Por ello, debemos pensar que la primera ley de Kepler es un resumen de las observaciones realizadas, es decir, una ley empírica. Pero, aunque esta ley nos da cuenta de todas las localizaciones de un planeta, no nos dice nada acerca de cuándo será ese planeta en uno u otro lugar, es decir, nos indica la imagen de la órbita, pero su velocidad no. Por lo tanto, esta ley se queda muy corta porque los astrónomos (y Kepler también) quieren saber de antemano cuándo será un planeta en un punto. Por eso, antes de que salga su primera ley, Kepler tenía establecida una segunda ley que nos indica los cambios en la velocidad de un planeta.

Kepler sabía que si existiera una relación matemática entre la velocidad de una y otra posición de la órbita de un planeta, el sistema sería mucho más sencillo. Si se descubriera esta relación, el movimiento de un planeta se podía expresar con muy pocos datos. Se necesitaban dos datos para proporcionar la misma elipse, el tercero para alcanzar la velocidad en un punto concreto del recorrido (en el perihelio, por ejemplo, el punto más cercano al Sol) y otro para conocer la inclinación del plano orbital respecto a otros planetas. Pero nadie conocía esa relación. Por eso, cuando se le ocurrió esta ley se dice que estaba en el éxtasis, pero lo que sabemos es que para encontrarla tuvo que analizar un montón de datos y realizar un trabajo constante y duro.
En cualquier caso, el camino que siguió para conseguir esta segunda ley es sorprendente, ya que en base a las tres erróneas hipótesis llegó a su conclusión. En palabras de Kepler, la órbita que describen los planetas se debe a la fuerza que ejerce el Sol y cuyo valor era inversamente proporcional a la distancia entre el Sol y el planeta. La velocidad y la fuerza que impulsa el planeta eran directamente proporcionales entre sí y, por tanto, inversamente proporcionales a la distancia. Esta hipótesis (es decir, que la velocidad sea proporcional a la fuerza) es hoy inaceptable, pero se puede ver como la idea de Aristóteles o como algo que el sentido común daba en aquella época.
Según esta hipótesis, el tiempo que tarda un planeta en recorrer una pequeña distancia durante el recorrido sería proporcional a la distancia al Sol. Esto es casi totalmente correcto y así en algunos puntos de la órbita. Por lo tanto, Kepler quería calcular el tiempo necesario para completar un gran tramo de recorrido (y por lo tanto cuando la distancia al Sol es variable). Para ello, tuvo en cuenta las distancias de todos los pequeños arcos que forman este gran tramo y concluyó que ese tiempo es directamente proporcional a la superficie que cubre la línea que va desde el Sol hasta el planeta. Según esta segunda ley, la Tierra (o si se quiere el Sol en el fondo de las estrellas) se entiende que en invierno se mueve más rápido que en verano, algo que tanto Kepler como sus predecesores conocían perfectamente.
Ambas leyes fueron publicadas en 1609 en el libro Astronomía Nova. Pero Kepler no gustaba y tenía una preocupación: no se conocía ninguna relación entre los movimientos de los diferentes planetas. Cada planeta se movía en su elipse y a su velocidad, pero parece que no había un modelo general para todos. Kepler pensaba que debía existir este modelo general, por lo que debía existir una relación que relacione todos los movimientos presentes en el sistema solar. Kepler partió tras esta relación y para ello utilizó la teoría musical, según los seguidores de Pitágoras, en busca de un vínculo entre las órbitas de los planetas y las notas musicales. Si su prolífica obra se llamó La armonía del mundo, quería expresar algo.
Creer en esa relación (o mejor dicho, su obsesión) puede, por un lado, expresar la primera fe mágica de los números que tenía Kepler, pero también la tendencia de todos los genios de la ciencia. Según ellos, la Naturaleza es uniforme y sencilla. Esta creencia ha dado una gran ayuda a los científicos y una fuerza para superar los obstáculos. Ése es el caso de Kepler, que tras descubrir su tercera ley por haber sufrido mil desgracias personales, fue capaz de escribir:

... después de haber encontrado durante mucho tiempo una distancia real de las órbitas utilizando los datos de Brahe, una relación real... el hecho de que exista un consenso tan amplio entre el trabajo que presento hoy en día y el trabajo que yo he realizado durante diecisiete años sobre las observaciones de Brahe, limpió mis sombras de mi mente y pensaba que al principio estaba en mis sueños...
Según el lenguaje actual de esta ley, si el período de un planeta es T (es decir, el tiempo de dar una vuelta completa alrededor del Sol) y R su radio medio, T 2 = K . R es 3, siendo K una constante igual para todos los planetas. En el caso de la Tierra T = 1 año y R = 15 x 10 7 km, por lo que si conocemos su radio R para cualquier otro planeta, podemos encontrar el periodo.
Esta tercera ley se llama ley armónica, porque representa una bonita relación armónica entre los planetas.
A través de todo ello, relacionando lógicamente nuestro sistema solar, lo vemos como un todo simple: nuestra inteligencia capta el universo de Kepler con una mirada y es capaz de expresar matemáticamente las leyes que lo rigen.
Kepler, a partir de los datos de Brahe, intentó construir tablas detalladas de movimientos planetarios. Para llevar a cabo esta labor tuvo que abandonar algunas de las opiniones aceptadas en aquella época. Esta actitud era completamente nueva, es decir, dar prioridad a las observaciones, si éstas se realizaban de forma precisa y cuantitativa. Otro aspecto a destacar es la predicción del uso del lenguaje matemático en la expresión de leyes físicas. Posteriormente, las ecuaciones serían las expresiones naturales de las leyes físicas.
Por otra parte, el movimiento de los planetas en su órbita en el sistema de Kepler no se consideraba producido por ningún dios (como lo demostraban los escolásticos), ni por sus formas esféricas representaban movimientos circulares. En su último libro ( Mysterium Cosmographicum ) nos cuenta cómo cambió sus opiniones en 1596:

En una época creía firmemente que la fuerza del movimiento de un planeta estaba en un alma... Sin embargo, cuando pensé que esta causa del movimiento disminuía con la distancia (es decir, como la luz del Sol disminuye con la distancia a este astro), llegué a la conclusión de que esa fuerza debía ser substancial, no literalmente, sino… como decimos que la luz es algo substancial, es decir, algo no espiritual y que sale de un cuerpo substancial.
En 1605 escribe a un amigo:
Me he ocupado mucho de la investigación de causas físicas. Mi ensayo ha consistido en demostrar que la máquina celeste debe compararse con un organismo divino y no con una obra de relojería (y quien cree que un reloj tiene alma, atribuye el honor al relojero), y que en ese reloj todos los movimientos diferentes son el resultado de una simple fuerza magnética, como todos los movimientos de la máquina de un reloj son consecuencia de un único peso. Además, demostro que esta concepción física debe expresarse mediante cálculo y geometría.
En Kepler podemos ver claramente el cambio iniciado en Europa dos siglos antes. La observación día a día, los resultados, en definitiva, dejan paso a las simples especulaciones y las teorías tienen que basarse en esa realidad. Por eso podemos decir que Kepler hizo una primera reivindicación de la actitud moderna de la ciencia.





