Vaches d'Archimède
Mais son hobby ne se référait pas à des problèmes mathématiques profondes. Au contraire, Archimède a également abordé l'aspect ludique des mathématiques. Le problème des vaches en est un exemple.
Les mathématiques classiques nous ont laissé des problèmes de résolution difficile (quadrature du cercle, trisection de l'angle, théorèmes de Fermat, ...). Avec de nouvelles idées ou des raisonnements ingénieux, beaucoup d'entre eux ont été résolus ou ont été révélés insolubles. D'autres, cependant, attendent toujours une réponse. Il est surprenant que, parmi tant de problèmes, les problèmes d'Archimède n'ont besoin que de calculs. Pour pouvoir faire ces calculs, il a fallu 2000 ans. C'étaient des calculs si lourds que seul l'ordinateur pouvait résister.
a.C. III. Nous sommes au 20ème siècle, Archimède a donné une approximation au nombre:
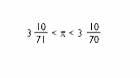
La clé Apollonius, en plus d'offrir une meilleure approche, a critiqué le travail d'Archimède dans le traité sur la multiplication de grands nombres. Archimède, accablé par des faits antérieurs, prépare une vengeance en inventant et en envoyant un problème difficile qui a besoin de grands nombres, dont il domine ses concurrents. La réponse d'Apollonius est inconnue, mais il a également envoyé le problème à Eratosthène, le bibliothécaire d'Alexandrie, et grâce à cela, il est venu à nos mains.
Tout cela est légende et nous ne savons pas si c'est vrai ou non. D'autre part, le problème est, au moins, celui de C. II. Il est également admis qu'il est un subordonné et que les nombres à utiliser pour résoudre sont vraiment grands. La solution la plus petite, par exemple, a 206.545 chiffres.

L'énoncé complet du problème a été découvert en 1773 par Gotthold Ephraim Lessing dans une bibliothèque de Wolfenbüttel. Il était écrit en grec et composé de lignes parallèles. La synthèse peut être la suivante:
Il calcule, ami, le nombre de rayons solaires. Pensez à cela si vous avez des connaissances. Il calcule une fois le nombre de personnes séjournant dans les plaines siciliennes, divisées par couleurs en quatre groupes: l'un blanc, l'autre noir, l'autre rouge et la dernière peinture. Les taureaux étaient plus que des vaches, dans les conditions suivantes:
1. Taureaux blancs = taureaux rouges + (1/2 + 1/3) taureaux noirs.
2. Taureaux noirs = taureaux rouges + (1/4 + 1/5) taureaux peints.
3. Taureaux peints = taureaux rouges + (1/6 + 1/7) taureaux blancs.
4º Vaches blanches = (1/3 + 1/4) solde noir.
5. Vaches noires = (1/4 + 1/5) solde peint.
6º Vaches peintes = (1/5 + 1/6) solde rouge.
7. Vaches rouges = (1/6 + 1/7) solde blanc.
Si vous pouvez donner le nombre de vaches et de vaches pour chaque solde, ami, vous n'avez pas de rival entre les numéros. Mais vous ne pouvez pas encore faire partie du groupe des sages. Pour cela, vous devez tenir compte des relations suivantes entre les rayons solaires:
8º. Taureaux blancs + taureaux noirs = tout le carré (p2).
9. Taureaux peints + taureaux rouges = numéro triangulaire (n(n+1)/2).
Lorsque vous calcule tout le solde, alors, ami, inscrivez-vous à part entière et présumez que votre nom brille dans le monde de la connaissance.
Comme vous pouvez le voir, deux problèmes apparaissent dans un. Les sept premières conditions sont faciles à résoudre. Cependant, les neuf ont créé des difficultés pendant 2.000 ans.
Il faut noter que les deux acceptent des solutions infinies. Le problème est de chercher la solution la plus petite. La réalisation d'opérations algébriques permettra d'obtenir les résultats suivants:
Taureaux blancs = 10 366 482 K Taureaux noirs
= 7 460 514 K Taureaux rouges
= 7 358 060 K Taureaux rouges
= 4 149 387 K Vaches blanches
= 7 206 360 K Vaches noires
= 4 893 246 K Vaches rouges
= 3 515 820 K Vaches rouges
= 5 439 213 K
Dans les résultats précédents K est tout nombre naturel. En donnant des valeurs à K on obtient différentes solutions. La plus petite solution est obtenue en faisant K = 1. Dans ce cas, le nombre total d'animaux est de 50 389 082.
Quant au deuxième problème, il semble qu'à l'époque d'Archimède il n'y avait pas d'outils pour résoudre. Et c'est que jusqu'à il y a 100 ans aucun progrès n'a été réalisé. En 1880 A. L'Allemand Amthor a rendu les équations plus utiles et a dit que la solution commençait par 776 ... et a eu 206.542 chiffres. Il a réussi dans la première, mais dans la seconde il se trompait de 3 chiffres.
La première solution sans erreur a été obtenue en 1965 par ordinateur, mais n'a été publiée nulle part. Auteurs du programme H.C. Willians, S.A. German et C.R. Il s'agit des quais canadiens. En 1981 Harry L. L'Américain Nelson a employé le problème pour examiner l'ordinateur CRAY-1. Il a obtenu la solution en 10 minutes et l'a imprimée en 47 pages. Les 47 pages se trouvent dans le numéro 3 du volume 13 du magazine “Journal of Recreational Mathematics”.
Pourquoi les solutions du premier et du second problème sont-elles si différentes ? Remplir la condition 8 n'est pas si difficile. Les taureaux noirs et blancs totalisent 17 826 996 K. Par conséquent, en prenant K = 17 826 996, nous obtenons le carré complet. La difficulté survient lorsque l'état est pris en compte 9.
La condition 8 peut être écrite comme :
p 2 = 17 826 996 K
= 4 . 4 456 749 K;
maintenant, en choisissant K = 4 456 749 t 2 et en le remplaçant dans l'égalité précédente, vous obtenez:
p 2 = 4 . 4 456 749 4 456 749 t 2
= 2 . (4 456 749)2 . 2
= (2 . 4 456 749 t) 2 ,
c'est-à-dire, nous avons tout le carré. C'est le progrès que Amthon a obtenu. Ainsi, si K = 4 456 749 t2 est sélectionné, la condition 9 peut être écrite comme :
Taureaux peints + taureaux rouges = 51 285 802 909 803 . considérant que t 2
51 285 802 909 803 t 2 = n (n+1) / 2
n, étant t chiffres naturels.
(Nous recommandons au lecteur de ne pas chercher la solution de l'égalité précédente).
Ceux qui ont utilisé le problème d'Archimède pour tester le CRAY-1 n'ont pas aimé la première solution et ont commencé à chercher les cinq suivantes. La plus grande de ces cinq chiffres dépasse le million d'euros. Bon solde !
Notre question est comment pouvait-on vivre tant gagné en Sicile?





