Hasiera »   Erreportajeak »   Algoritmo genetikoak, soluzio egokienaren bila

Genetic algorithms in search of the most suitable solution

• Zabaldu:
• Twitter
• Facebook
• Emaila

Genetic algorithms are a programming technique that mimics biological evolution and is used to solve very difficult or impossible problems by conventional methods. They don't know very well why, but conventional techniques work in problems that fail, so they are increasingly used to solve practical problems.

In nature, the initially existing population changes over time. From generation to generation, some factors make the individuals who adapt worse disappear, while those who adapt better survive. Therefore, within the population the proportion of better increases. However, some who do not seem so good may continue to have a different strategy or by chance. And it could cross with others, as others cross. Therefore, it is possible that the characteristic of the supposedly bad individual will appear in the next generation in other members.

Occasionally another variable appears: the mutation. Although not very common, it influences the characteristics of the members of the population. Due to the crosses, mutations and agents that bet on the best, once the time has elapsed, the population is formed by the members better adapted to the environment.

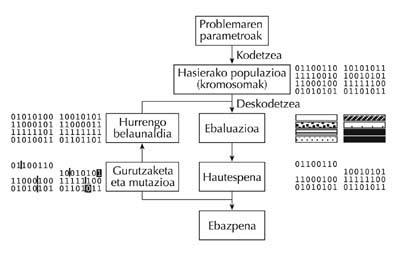
This is what Darwin explained more or less in the theory of species evolution, and it is what genetic algorithms do. The initial population consists of possible solutions to a problem. These possible solutions are randomly selected and called chromosomes. The different aspects of each chromosome are called genes.

If they are candidates, they are given a function that measures their suitability. As is normal, most candidates are inadequate, but others somehow work and stay.

The candidates who have advanced multiply and cross. Therefore, in the next generation, some have several copies and others have been wrong. In addition, a few are not exactly the same as the previous ones: they have changed, that is, they have randomly modified some gene.

The resulting generation is different from the previous one and the suitability of these candidates is measured. Thus, candidates who are no better than the previous ones are discarded, those who remain are better solutions than the initial ones. They reproduce and occur crosses and even mutations. The new candidates are evaluated and the best ones are re-elected, the process is repeated every hundred or thousand times. The resulting population is made up of very good solutions to the problem.

Numbers, letters and trees

To start working genetic algorithms it is necessary to code the possible solutions of the problem so that the computer can process it. One option is to encode in binary chains: They are strings formed by 1 and 0 and the digit in each place of the string represents the value of an aspect of the resolution.

Another way to encode is by strings of integers or decimals. As in the previous case, the number in each location indicates the value of a specific aspect of the resolution. You get more accuracy and complexity than with binary code, as it limits less than using two numbers. On the other hand, numbers can be replaced by letters to encode candidates.

With these three methods it is very easy to define operations that will randomly perform crosses and mutations between candidates; it is easy to put a 1 where there is a 0 or vice versa; add or remove a value to a number; or replace one letter with another.

In addition, there are other ways to code, such as that done with trees. Data is branched and changes are made by changing the value of patches or replacing some branches of the tree with others.

Selection and modification

Code one way or another, schedule the choice of individuals to copy for the next generation. The selection can be done in different ways and usually several of them are used at once. One of them is the elitist selection, that is, the selection of the best of each generation. Another form depends on the capacity: more capacity, more choice possibilities.

In addition, to ensure the diversity of the population, you can use a roulette wheel: each candidate has a portion of the roulette; more capacity, most adapts to the candidate. Turning the wheel, those who have a large part are more likely to be elected, but may adapt to a candidate with little capacity to be elected for the next generation. This ensures that the next generation is not too egalitarian.

Another way to ensure this is by conducting groups by level of competition and choosing the best of each group, so that the best of the low capacity group would advance. Teams can also be done randomly and then forced to compete with each other, the winners move on to the next generation.

There are other selection methods: staggered, hierarchical selection... In any case, the goal is that the candidates of the next generation are on average better than the previous ones. In addition, candidates selected for the next generation are made some random changes in the hope that better individuals will appear.

There are two ways to make the changes: mutation and crossing. Mutation is changing a specific aspect, a gene. The crossing consists of redeeming part of the code for another candidate. The "child" thus formed has in common the characteristics of the two "parents". It is therefore a recombination between paternal and maternal chromosomes in sexual reproduction.

For and against

Through selection, mutation and crossing, from generation to generation, genetic algorithms are approaching the solution of the problem. In many cases, the genetic algorithm will not be enough to release the problem, but it can provide reasonably good solutions, and applying the usual methods to this final population can obtain the best solution.

One of the advantages of genetic algorithms is that they are “blind”, that is, they know nothing about the problem they have to solve. More than an advantage may seem a disadvantage, but it is very good, as it does not reject from the beginning any candidate with a bad appearance. In addition, the cruise and mutation create surprising solutions. Somehow, prejudices do not affect genetic algorithms, they just care to move forward.

In addition, they work in parallel, that is, in different ways at once. Most algorithms work in series and can only move in one direction every time. When they realize that they have taken the wrong path, they have to abandon all the work and start over. However, genetic algorithms do not have this problem and are especially effective in solving problems with many possible solutions.

They have more advantages but also some drawbacks. The first is the difficulty of writing the definition of the problem. The coding of candidates is not simple and sometimes it is hard to write the function that measures the capacity. The size of the population, the frequency of mutations and crosses, as well as the type and force of selection, are very important factors in genetic algorithms, which if not designed well, do not advance.

Apps

Despite their limitations, they are used to solve problems such as acoustics, aerospace engineering, astronomy and astrophysics, chemistry, financial market, games, geophysics, material engineering, mathematics, molecular biology, telecommunications, etc.

For example, in 2002 researchers at Kobe University in Japan used genetic algorithms to design a music room. They left a room in the form of a shoe box and defined the parameters that should have to achieve the best acoustics. The algorithm gave two results, both in host form, which seem to have spectacular acoustics. According to the researchers, they are like the Grosser Musikvereinsaal in Vienna, the best in the world.

For its part, NASA has used them in the design of packaging, but also in the study of white dwarfs and in the design of schedules. In fact, genetic algorithms are very effective for carrying out schedules in both companies, airports and schools.

In schools, for example, the right time is a problem. One teacher per classroom is required and one teacher cannot be in two classrooms simultaneously. Of course, each teacher has to give his subject and, perhaps, some subjects better than one hour and not another (it is not advisable to put at the last minute mathematics, physics, etc. ). In addition, the preferences or needs of teachers must be taken into account. Since so many factors must be taken into account, it is very difficult to get a good schedule in large centers. Well, genetic algorithms are perfect.

The experts have no doubt that, even though they are relatively new (the first appeared in the 1960s), they have had a rapid development and, according to the mathematical Mª Teresa Iglesias, "do not stop them".