Regulation of use of the Chinese abaco (I). Addition, subtraction and multiplication
Elhuyar. In number 42 of Science and Technology we will continue with the path started with the abacus giving guidelines for the use of Chinese abacus. We will describe the basic operations: addition, subtraction and multiplication (in number 43), division (in number 44) and square and cubic root (in number 45).
In the previous issue we describe the abacus of China, called bread. Remember that each column represents a recomposition of ten; starting with the right, units, tens, percentages, thousands, etc. We will not leave columns for tenths and hundredths. We know that each ball at the bottom will have a tenth of one of its columns on the left and at the same time one of its columns on the right will have a value of ten times. A top ball is worth five times that of the bottom of the same column.
To move the balls, it is said that the best way is to operate the upper balls with the middle fingers and the lower balls with thumb (up) and index (down).
Starting position: upper balls above, next to the outer ribbon or strabe and lower balls below, next to the lower strabe. The last balls above and below (next to the stirrups) to join and remove should not be used: the upper balls (the two) represent ten units of the order and the same a lower ball of the left column. Therefore, instead of lowering the top ball will raise one of the lower balls of the left column. Something similar happens with the lower balls: instead of raising the fifth, a top ball of the same order equivalent to five balls will descend. Hence the disappearance of these two balls in the Japanese countryside.
There is a basic difference between written arithmetic and abacus arithmetic. In the first the operations begin on the right and in the second on the left.
To check the calculations we recommend that you repeat them once.
Before starting operations, indicate the following numbers to practice:
1427; 7593; 500005; 137005; 10010; 16896; 170; 61340; 400271 and all you want.
Addition
The sum is completed with seventeen rules. These rules should be used when there are not as many balls as you have to add in each column when making the sum. Before we explain the words that we will use.
- Lower 5 cm towards the interval estrabe - move a top ball.
- remove - remove a ball located before on the sides of the interval layer?
- up a lower ball towards the intermediate layer.
- Forward ten - raise a bottom ball of the left column.
The first number of each rule indicates the number to be added to an existing number. For example, in a column we have the number 4 and we want to add the 2. Let's go to the second rule: lower five, remove three, i.e. move a top ball down and remove three lower balls from the intermediate layer.
Collection rules
- BAT: download five, delete four
- TWO: lower five, remove three
- HIRU: down five, remove two
- FOUR: down five, remove one
- BAT: eliminate nine overtake
- TWO: remove eight, advance ten
- HIRU: eliminate seven, advance ten
- FOUR: eliminate six, advance ten
- FIVE: delete five, advance ten
- SIX: delete four, advance ten
- SEVEN: eliminate three, advance ten
- EIGHT: remove two, advance ten
- NINE: remove one, advance ten
- SIX: upload one, delete five, advance ten
- SEVEN: two climbs, five climbs, ten advanced
- EIGHT: three climb, five eliminate, ten overtake
- NINE: four raise, five delete, ten overtake
Exercises:
24 + 36783
+ 275 + 14 + 5697 + 341 +
2 + 3 + 4 + 5 + 7 + 8 + 9312,75 + 21,
03 + 2304,69 (leave the two columns on the right for the tenths and hundredths).
Subtraction
As in the sum, here there are also 17 contrary rules. In each rule the first number to be removed.
ten delete - remove a bottom ball from the left column
Withdrawal rules
- BAT: delete five, return four
- TWO: delete five, return three
- THIRD: delete five, return two
- FOUR: delete five, return one
- BAT: ten delete, nine return
- TWO: ten delete, eight return
- THIRD: ten delete, seven return
- FOUR: delete ten, return six
- FIVE: delete ten, return five
- SIX: delete ten, return four
- SEVEN: delete ten, return three
- EIGHT: delete ten, return two
- NINE: delete ten, return one
- SIX: delete ten, return five, delete one
- SEVEN: remove ten, return five, remove two
- EIGHT: remove ten, return five, remove three
- NINE: remove ten, return five, delete four
Exercises:
(3402731 - 1924005) - 71913884
- 4987136 -
5328
Remember that these two operations must start on the left.
Multiplication
In order to carry out the multiplication without it is necessary to know the basic multiplication table from 1 x 1 to 9 x 9.
The multiplier is located on the left side, the product on the right side, leaving as many columns free as number of multiplier figures. In these free columns, product units, tens, percentages, etc. remain.
Multiplier of a figure
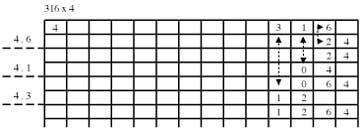
Let us multiply number 316 by number 4. The right column must be empty and the 316 2. Place in columns 3 and 4. (see table below).
4. 6 = 24; 4 in the free column, 6 in the second column and
2 in the second column4. 1 = 4; add 4 to 2 from the second column and remove 1 from the third column
4. 3 = 12; add 2 to zero of the third column and in the fourth remove 3 and put 1.
You will get 1264 results.
- Note: the decimals of partial products (2, 0, 1) are written instead of the multiplied number (6, 1, 3) and units (4, 4, 2) are added to the right number of this (0, 2, 0). The number multiplied by each partial
operation (6, 1, 3) must be removed. - Note: this method is called the final opening. You could also use the initial opening method to multiply, but the first one is better.
Exercises
617283945
3086419725 205761315
6;4115263
3;246913574 17636684
7;15432096625 8;13716421
9;271980079
Safety
Logically, by multiplying by the power of ten the multiplier zeros are added.
Multiplier with several figures
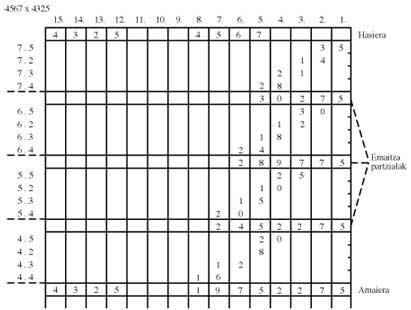
4567. To multiply 4325 we will write 4325 to the left and leave four columns to the right to put the numbers 7, 6, 5 and 4 in columns 5, 6, 7 and 8. Number 7 is multiplied by 5, 2, 3, 4 and written from right to left. The same with numbers 6, 5 and 4 but leaving to the right a column, two and three free. Keep in mind that the figure of the product used (7, 6, 5, 4) disappears in partial results.
7. 5 = 35 in the first column 5 and 3 in the second column.
7. 2 = 14 the first column equal, 3 the second with 4 (7) and the third with 1
. 3 = 21 Add 1i (2) of the third column and 2 in the fourth 7. 4 = 28 to 2 of the fourth column add 8 (10) and in the fifth
7 write
2 + 8 = 10, write 0 and add 2 from the left 1 + 2 = 3
The same with other numbers. (see table above).
- Note: when the multiplier has a 0 it does not multiply, but you have to save the corresponding gap.
Exercises:
345.
27;369 63;5241
345;5234
739;38613 30;58235
5802;7198 4957