Trece nuevas soluciones al problema de los tres cuerpos
Newton encontró el problema cuando publicó la ley de la gravedad. Cuando se analizan dos cuerpos, como una estrella y un planeta en la órbita circundante, no hay problema: el cálculo del movimiento es exacto. Each contains repetitions órbits on the mass centre. Pero cuando se añade un tercer cuerpo al sistema, como el Sol, la Tierra y la Luna, no es posible calcular las periodicidades de los movimientos de los tres. No es posible, así lo demostró el matemático Heinrich Bruns en el XIX. A finales del siglo XX. Y mucho menos para el caso en el que se pasa de tres cuerpos a muchos cuerpos.
Esto significa, por ejemplo, que no es posible determinar matemáticamente los movimientos de los planetas del sistema solar a través de las ecuaciones de las órbitas. Siempre habrá que añadir correcciones en los movimientos calculados para ellos. Para calcular cuándo se producirán los eclipses y desde dónde se van a ver también es necesario realizar cálculos complejos. Y fuera de la astronomía también influye el problema, ya que existe la misma dificultad para calcular los movimientos de las tres partículas.
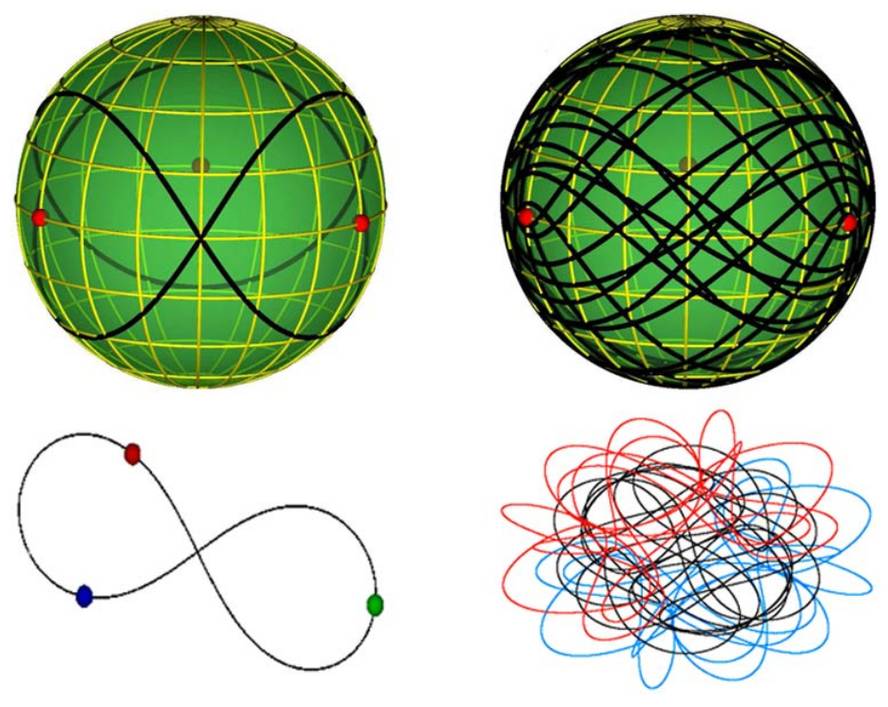
Sin embargo, en casos concretos y particulares se puede encontrar solución. XVIII. En el siglo XIX, los famosos matemáticos Euler y Lagrange resolvieron el problema para el caso de que uno de los tres cuerpos tuviera muy poca masa y teniendo en cuenta el movimiento sobre una circunferencia. En la década de 1970, el matemático Roger Brouke y el astrónomo Michel Henon calcularon una solución para otro tipo de casos: cuando uno de los tres cuerpos se mueve en órbita alrededor de los otros dos. Y en 1993, el físico Cristopher Moore encontró un tercer tipo de solución para los movimientos ochomiles.
Hasta el momento, sólo estas tres familias de soluciones han sido posibles para el problema de los tres cuerpos. Ahora, sin embargo, ha habido una revolución: Físicos de la Universidad de Belgrado han encontrado muchas nuevas soluciones. Su técnica consistía en partir de soluciones concretas, modificando progresivamente las condiciones iniciales de los movimientos de los tres cuerpos hasta encontrar una nueva solución. Los físicos están sorprendidos porque esta técnica ha dado muchos resultados. De hecho, las soluciones que han obtenido han tenido que clasificarlas en trece familias diferentes. Esto significa que ya hay dieciséis familias de soluciones para el problema de los tres cuerpos.