Hasiera »   Albisteak »   Hamahiru soluzio berri hiru gorputzen problemari

Thirteen new solutions to the problem of the three bodies

• Zabaldu:
• Twitter
• Facebook
• Emaila

Physicists at the University of Belgrade have discovered many new solutions to the problem of the three bodies. The problem itself does not have a general solution, but in certain special cases, in which physicists have found many of these special cases and have classified solutions into thirteen families.

Newton found the problem when he published the law of gravity. When two bodies are analyzed, such as a star and a planet in the surrounding orbit, there is no problem: the calculation of motion is accurate. Each contains repetitions orbits on the mass centre. But when a third body is added to the system, such as the Sun, Earth and Moon, it is not possible to calculate the periodities of the movements of the three. It is not possible, as demonstrated by the mathematician Heinrich Bruns in the XIX. At the end of the twentieth century. And much less for the case in which it is passed from three bodies to many bodies.

This means, for example, that it is not possible to mathematically determine the movements of the planets of the solar system through the equations of orbits. Always add corrections in the movements calculated for them. To calculate when eclipses will occur and from where they are going to be seen, complex calculations are also necessary. And outside astronomy also influences the problem, since there is the same difficulty in calculating the movements of the three particles.

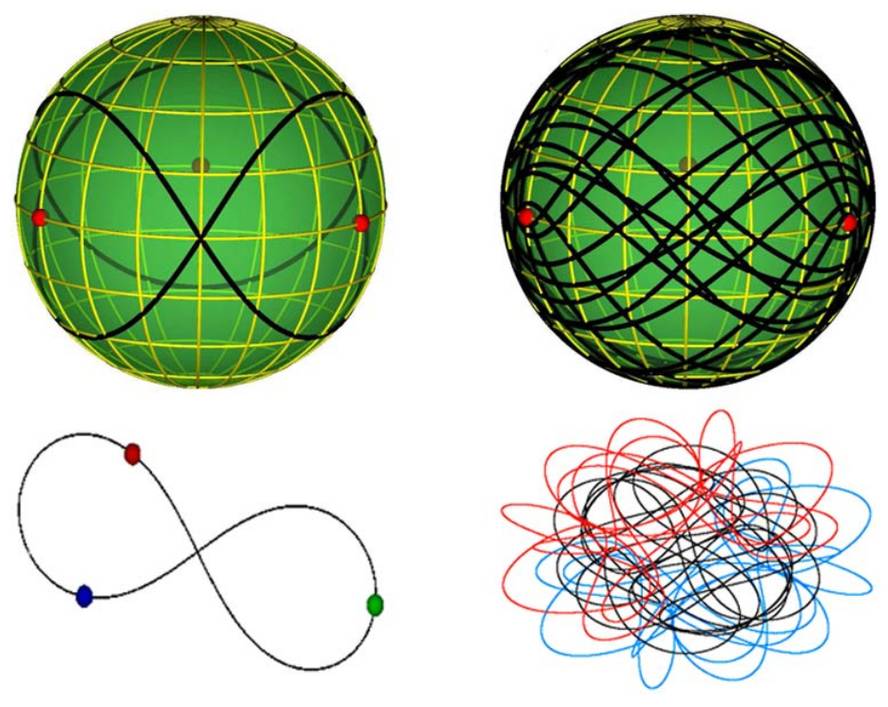
However, in specific and particular cases, a solution can be found. XVIII. In the nineteenth century, the famous mathematicians Euler and Lagrange solved the problem for the case that one of the three bodies had very little mass and taking into account the movement circumference. In the 1970s, mathematician Roger Brouke and astronomer Michel Henon calculated a solution for another type of case: when one of the three bodies moves in orbit around the other two. And in 1993, physicist Cristopher Moore found a third type of solution for the eighties movements.

So far, only these three families of solutions have been possible for the problem of the three bodies. Now, however, there has been a revolution: Physicists at the University of Belgrade have found many new solutions. His technique consisted of concrete solutions, progressively modifying the initial conditions of the movements of the three bodies until finding a new solution. Physicists are surprised because this technique has given many results. In fact, the solutions they have obtained have had to classify them into thirteen different families. This means that there are already sixteen families of solutions for the problem of the three bodies.