Claude Shannon, pare del món digital
Preguntats per les persones més importants del món de les Tecnologies de la Informació i la Comunicació, la majoria de la gent probablement no serà capaç de donar noms més enllà de Bill Gates, Steve Jobs, etc. Els que coneixem millor el món de la informàtica segurament diríem altres noms com Alan Turing o Tim Berners-Lee. Entre nosaltres potser no tant esmentarien a Claude Shannon. No sabem quina és la raó, però Shannon no té en absolut la fama que mereixen les seves immenses aportacions; Shannon, per exemple, serà el nom més important del món de les TIC.
Claude Elwood va néixer el 30 d'abril de 1916 en un poblet de l'estat nord-americà de Michigan. Des de la seva infància va ensenyar a l'escola la competència en ciència i matemàtiques, així com l'afició per la invenció i construcció de dispositius mecànics i elèctrics. Així, en 1932, amb tan sols 16 anys, comença els seus estudis universitaris en la Universitat de Michigan, i en 1936 acaba les seves carreres de matemàtiques i enginyeria elèctrica. Posteriorment, en 1936, va començar a cursar un màster en enginyeria elèctrica en el prestigiós Massachusetts Institute of Technology o MIT. I en 1940 va defensar la tesi doctoral en matemàtiques en aquesta mateixa institució.
Fonaments d'Electrònica Digital
No obstant això, la primera de les seves dues majors aportacions a la ciència la va realitzar abans de la tesi, concretament en el projecte de màster, amb tan sols 21 anys. Segons diversos experts, va ser la tesi de màster més important de la història.
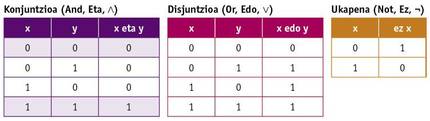
Durant la realització del màster, Shannon va poder treballar amb un dels ordinadors més potents de l'època, l'analitzador diferencial de Vannevar Bush. Aquells ordinadors de llavors eren analògics, funcionaven amb corrioles, engranatges, etc. i ocupaven un gran espai. També va tenir l'oportunitat de conèixer l'àlgebra de Boole en els seus estudis de matemàtiques. En l'àlgebra de Boole les variables no tenen valor numèric sinó Veritat i Mentida (o 0 i 1), i les operacions bàsiques no són suma i multiplicació, sinó conjunció, disjunció i negació (And, Or i Not). Aquestes operacions es defineixen mitjançant les següents taules de la veritat:
Shannon va dissenyar en el projecte del màster circuits elèctrics d'interruptors que implementaven l'àlgebra de Boole. A més, va demostrar que les combinacions d'aquests circuits permetien realitzar qualsevol operació matemàtica o lògica i va dissenyar alguns d'ells. Aquest treball va establir les bases per al disseny de circuits digitals i d'aquí va sorgir l'electrònica digital. L'ordinador i tots els altres dispositius electrònics i digitals han vingut gràcies a la visió que va tenir en el projecte del seu màster.
Teoria de la informació, base de l'emmagatzematge d'informació i comunicació digital
A pesar que aquesta aportació és realment impressionant i sorprenent, es considera la seva aportació més important. Shannon és sobretot conegut per la creació d'un camp de coneixement de la teoria de la informació i pel seu desenvolupament gairebé complet, en 1948, quan treballava en prestigiosos laboratoris Bell, va escriure en el seu article “A mathematical theory of communication”.
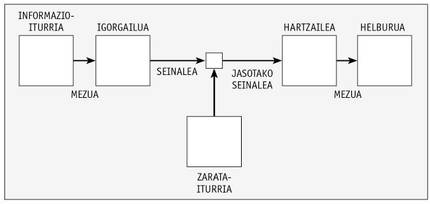
En aquest article, Shannon va definir un sistema de comunicació a través de la imatge inferior.
Així, analitza i proposa formes per a codificar el missatge de la manera més adequada. La imatge es pot aplicar de la mateixa manera a un sistema d'emmagatzematge en el qual s'escriu una informació en un mitjà en el qual el senyal emmagatzemat en el mateix pot sofrir una degradació i ha de ser la mateixa que la informació escrita en llegir.
En l'article, Shannon va proposar convertir la informació en base binària per a l'emmagatzematge i transport de la informació, és a dir, mitjançant els números 0 i 1. A aquestes unitats d'informació se'ls va indicar per primera vegada en aquest article binary digit o bit, encara que el nom fos J. W. Era la proposta de Tukey, company de Shannon.
Convertir la informació en digital era un gran avanç. De fet, la informació analògica que s'utilitzava fins al moment té més situacions possibles (infinites en realitat), i atès que la diferència d'una situació a una altra és petita, tot soroll o petit canvi en l'emmagatzematge o transmissió fa que un senyal es converteixi en una altra i és impossible recuperar la informació exacta original. Això ocasionava grans problemes en la transmissió dels senyals, per exemple, fins i tot aixecant periòdicament la potència del senyal amb repetidors, ja que es produïa una degradació i pèrdua d'informació irreparable. Per contra, traslladant la informació a la base binària, només existeixen dues situacions possibles, 0 i 1, i la diferència entre ambdues pot ser tan gran com es desitgi en el senyal físic (per exemple, 0 volts i 5 volts). Així, encara que el senyal es degradi o modifica lleugerament, és més difícil convertir un 0 en un 1 o viceversa. D'aquesta manera, la informació s'emmagatzema de forma més senzilla i fiable, i la transmissió es pot realitzar tan lluny com es desitgi mitjançant repetidors, sense perdre informació.
Això, per part seva, suposava un gran avanç, però Shannon va ser més enllà, definint pràcticament totes les tècniques i fórmules matemàtiques per als mètodes actuals de compressió i fiabilitat en emmagatzematge i comunicacions.
Per a això va definir diversos conceptes. Una d'elles és la informació que emet un missatge. De fet, Shannon va dir que no tots els missatges donen la mateixa informació: com més probable és un missatge entre tots els possibles, menys informació dóna. Així mateix, entre els símbols o caràcters d'un missatge, un símbol més freqüent facilita menys informació. Per a mesurar la informació d'un símbol va donar la fórmula I = –log2 p, on p és la probabilitat o freqüència del símbol. Aquesta mesura d'informació, a més, indica el nombre de bits necessaris per a transmetre aquest símbol. Així, necessitaríem un bit per a indicar cadascun dels dos resultats (leon o kastillo) que es poden obtenir en llançar una moneda, segons la fórmula. O per a representar cadascuna de les lletres d'un alfabet de 27 lletres, si tots tinguessin la mateixa probabilitat, serien necessaris 4,76 bits.
També va definir l'entropia d'un missatge. L'entropia del missatge és la informació mitjana que conté un missatge, per la qual cosa es defineix com: H =|Pi log2 pi. A més, atès que alguns dels símbols són més probables en uns contextos que en uns altres (en el cas de les lletres, per exemple, l'habitual és que després de la q vagi la lletra u, o que després de les consonants és més normal que una vocal que una altra consonant), Shannon va definir també una entropia condicionada en la qual es té en compte el signe anterior per a calcular les probabilitats. Doncs bé, aquesta mesura de l'entropia ens diu fins a quin punt un missatge es pot comprimir sense perdre informació! En els missatges de llenguatge natural, per exemple, tenint en compte les freqüències de les lletres i les freqüències condicionades, l'entropia és menor que una, per la qual cosa cada lletra pot codificar-se en senyals de menys d'un bit. I com ho va fer Shannon. Els sistemes de compressió sense pèrdues (ZIP, RAR o molts altres que s'utilitzen en les comunicacions…) que tant s'utilitzen en l'actualitat estan basats en fórmules i mètodes de Shannon.
Poc amb això, Shannon va teoritzar també sobre la compressió amb pèrdua, i tots els sistemes que utilitzen aquest tipus de compressió (JPG, MP3, DivX…) ho tenen bàsicament.
I per si no fos prou, també va escriure en aquest article sobre codis que detecten i/o esmenen errors. Per a detectar possibles errors o esmenar errors en una informació rebuda o llegida s'envia fonamentalment informació addicional redundant. Exemple d'això són els números de control en els números de compte o lletres que han afegit al número del DNI espanyol. Aquestes són, en definitiva, les sumes de checksum o control. Si hem fallat en algun número, la suma de control no coincidirà i sabrem que hi ha un error en el número. Per a esmenar l'error haurem de revisar manualment ja que en aquests exemples només s'utilitza el codi per a detectar errors.
Però existeix la possibilitat de completar el missatge original encara que hi hagi errors en el missatge rebut. Per a això és necessari introduir més informació addicional redundant i, sobretot, que totes les paraules o números possibles que es puguin enviar en el codi tinguin una distància mínima entre si. Així, suposem que la distància entre tots els caràcters possibles és de tres bits, si es produeix un error en un bit podem saber amb suficient certesa quin era el caràcter que es volia enviar, si la probabilitat de rebre dos bits erronis d'un senyal és relativament petita. D'aquesta forma, depenent de la fiabilitat del canal, realitzarem una major o menor distància entre els senyals del codi (nombre de bits) i introduirem més o menys informació redundant, però el receptor podrà també reparar els missatges erronis.
Els codis que corregeixen errors no els va inventar Shannon. El seu company Richard Hamming era el pioner en això. Però Shannon va formalitzar matemàticament la teoria dels codis de correcció d'errors i va definir el nombre màxim de bits addicionals necessaris per a diferents probabilitats de fallada del canal. I aquesta formulació és la que utilitzen tots els codis capaços avui dia d'esmenar els errors, amb milers d'usos: en les comunicacions amb naus espacials i unes altres, en l'emmagatzematge d'informació en CDs i pendrives, etc.
Com veieu, les aportacions de Shannon en l'article “A mathematical theory of communication” van ser ingents. Se li va avançar molt el seu temps, va proposar solucions a molts problemes pràctics de futur i tot d'una manera molt elegant, amb fórmules i teoremes matemàtics i demostrant teoremes.
...i més encara

A més d'aquestes aportacions principals, Shannon va realitzar moltes altres petites aportacions. “Txiki”, per dir-ho d'alguna manera, ja que són petits en comparació amb altres aportacions, però algunes d'elles serien suficients per a qualsevol altra fama.
II. Durant la Guerra Mundial, abans d'escriure el seu conegut article, Bell va treballar en criptografia en els laboratoris i va realitzar alguns descobriments en el camp de la criptografia. Això li va permetre conèixer a Alan Turing. Turing va parlar de la idea de la seva màquina universal, del concepte d'ordinadors actuals, que, en definitiva, es complementava perfectament amb les idees de Shannon. En aquella època, Shannon va inventar diagrames de flux de senyals.
Shannon li agradava els escacs i també va treballar en això. En 1950 va escriure un dels primers articles sobre la problemàtica dels programes d'escacs dels ordinadors, que va posar en marxa l'àrea. En aquest article va estimar que les combinacions possibles del joc d'escacs són almenys 10 120, la qual cosa avui es coneix com a número de Shannon.
En 1950 realitza el ratolí automàtic Theseus, capaç de trobar la sortida d'un laberint i aprèn el camí per a després. Es tracta del primer dispositiu d'intel·ligència artificial d'aquest tipus. També li agradaven els malabarismes i en els anys 70 va construir el primer robot malabarista. També va construir una màquina que resolia el cub de Rubik.
En els seus viatges a Las Vegas al costat d'alguns dels seus companys va guanyar una fortuna, ja que, aplicant la teoria del joc, comptaven cartes i van fabricar un petit i escondible ordenador (el que alguns consideren el primer wearable) per a calcular probabilitats en el joc. I amb mètodes similars van aconseguir guanyar encara més en bossa.
Shannon va morir en 2001, després d'haver sofert l'alzheimer en els últims anys. Per a quan va perdre la consciència de l'entorn, les seves aportacions ja van tenir nombroses aplicacions, però no va tenir l'oportunitat de conèixer el progrés i, sobretot, la difusió que han tingut en els últims anys Internet, els ordinadors i altres dispositius. Segurament se sorprendria. Com nosaltres hauríem de sorprendre'ns, perquè la persona que va permetre dur a terme aquest enorme canvi és gairebé desconeguda.