Pintxo-pote kontuak, blockchain a eta bitcoin
Els beneficis d'Internet són innegables. Per primera vegada disposem d'una eina que connecta a tota la societat. No obstant això, aquesta connexió ha creat un nou paradigma. Els usuaris no podem saber si la persona que està a l'altre costat de la xarxa és fiable. Per tant, com podem aconseguir que tots compartim informació sense que ningú substitueixi la identitat de ningú i canviï la informació privada?
En aquest article s'analitzarà la solució més coneguda que s'ha trobat en els últims anys per a solucionar aquest problema, prenent com a exemple la realització de comptes amb amics com el blockchain o les cadenes de blocs[3][6]. Per a això, en primer lloc, s'exposaran una sèrie de conceptes imprescindibles per a entendre què són les cadenes de blocs, així com els beneficis i problemes que poden suposar.
Què són les cadenes de blocs?
Imaginem que estem amb amics, per exemple, en el pot de pintxos del barri donostiarra de Gros. Com paguem els nostres pots de pintxos? D'una banda, és possible que cadascun pagui el seu, però és clar que no és l'opció més eficient, ja que ens costaria molt temps pagar. Una altra opció seria posar un pot entre tots, perquè així pagaríem molt més ràpid. Tanmateix, això planteja altres problemes: què passaria si els diners de la llauna no fos suficient? I si està sobrant al final? Moltes vegades no tots els preus són iguals, en aquest cas, com distribuiríem el preu?
A la vista d'aquests problemes podem pensar en una solució més adequada. Crearem un compte en la qual cadascun dels membres posi en cada bar quant deu i a qui deu. Perquè aquest compte sigui el més transparent possible, en lloc d'estar escrita en un paper, totes les dades estaran online perquè tots puguin veure'ls, per exemple, en un grup de WhatsApp. Però què passaria si els membres de l'equip no fossin fiables? Vegem quins trucs podem utilitzar per a solucionar aquest problema de fiabilitat. Al cap i a la fi, la cadena de blocs és només aquesta, un compte enorme que tot participant pot utilitzar per a escriure transaccions entre ells. Vegem, per tant, què és una transacció.
Transacció
Com ja s'ha indicat, apareixerà en el compte quant i a qui deu cada persona en cada bar. Hi ha dues maneres de fer-ho: que qui paga ho anoti en el compte o qui ho deu ho escriu. És clar que la primera opció no és convenient, ja que si algun participant faltés diners es podria posar en compte que uns altres li deuen. Per tant, serà el deutor qui anoti l'import i a qui deu. Així, assegurarem que ningú farà paranys perquè en escriure alguna cosa en el compte es perd diners. Això es denomina transacció en les cadenes de blocs. Però com podem saber si realment és capaç de pagar l'import que ha escrit? Molt fàcil. Cada vegada que s'escriu una transacció, cada persona que es trobi en aquest compte (en aquest cas en el grup WhatsApp) ha de comprovar si el deutor té la moneda suficient per a pagar la transacció. Si no és així, es cancel·la la transacció. I com podem saber si té suficient? Senzillament, perquè observant totes les transaccions anteriors podem saber si té suficient per a saldar el deute. En aquest punt ja podem detectar on està el valor del compte (en el nostre cas el grup WhatsApp): podem utilitzar en un nou pot de pintxos l'import que m'han degut prèviament. De totes maneres, com podem assegurar que només escric les meves transaccions?
Signatura digital
Signatura digital[1] sorgeix per a solucionar un únic problema: verificar l'origen d'un missatge. Encara que els éssers humans vegem un missatge com un conjunt de lletres, un ordinador veu un missatge com un conjunt de bits (qualsevol arxiu, francament).
Suposem que tenim molts usuaris. Els algorismes de creació de signatura digital són dues: el primer s'utilitza per a crear la signatura i el segon per a verificar la signatura. Cada usuari té dos codis anomenats clau, un privat (Iphone) i un altre públic (Gpu). La funció de creació de signatura és:
signa = signatura (missatge Iphone)
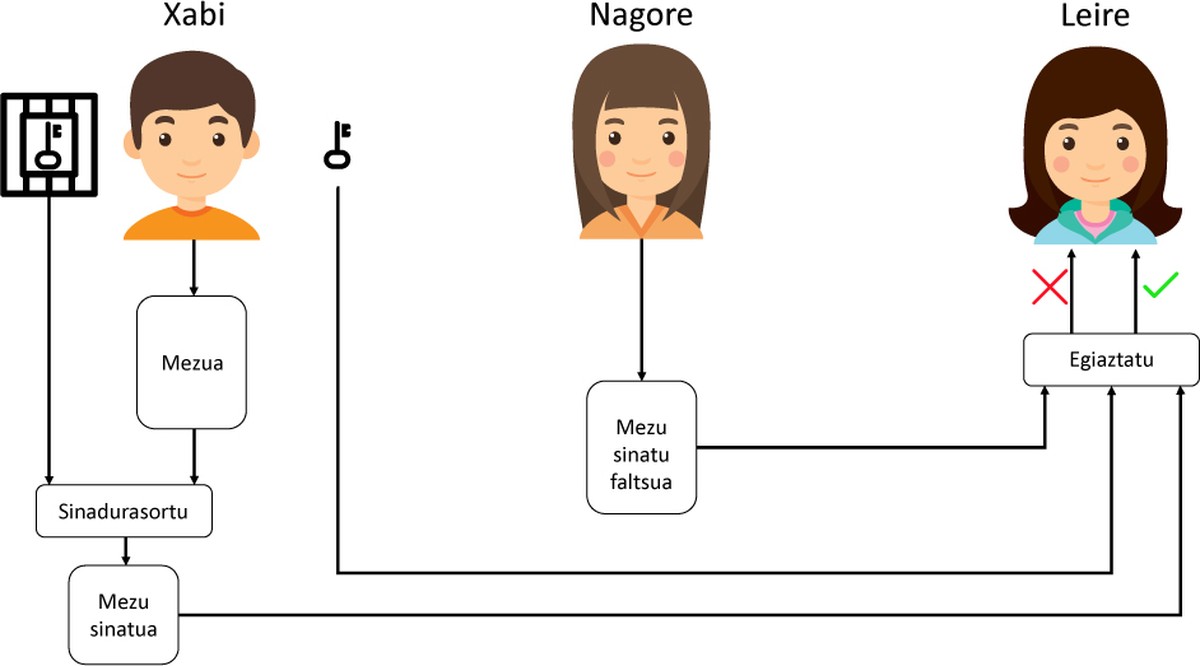
Aquí percebem la diferència més significativa entre la signatura de les persones i la signatura digital. Com pot veure's, cada signatura es crea per a cada missatge i usuari, per la qual cosa la signatura digital dependrà del missatge i de l'usuari (les persones utilitzem la mateixa signatura per a signar tots els documents). Això significa, entre altres coses, que podem utilitzar el nostre GPRS en diferents missatges sense perdre seguretat.
D'altra banda, tenim una altra funció de verificació de signatura:
si/no = comprovar(missatge, Gpu, signatura)
Aquesta funció ens indica l'origen de la signatura utilitzant la signatura, el missatge i la clau pública. D'aquesta forma senzilla podem saber si el missatge ha estat enviat per l'usuari que realment volem. A tall d'exemple, veure figura 1.
Bloc
El que hem dit fins ara seria útil en una quadrilla petita, i es podria aplicar sense problemes. Però normalment en el poteo de pintxos no solem estar amb la quadrilla, normalment ens trobem amb els de l'equip esportiu, de la universitat, dels membres del grup de ball... i en aquest cas no ens serveix el que hem fet amb la quadrilla. Fem llavors el grup WhatsApp de Sant Sebastià, un grup que englobi a tots els donostiarres. I hi ha algú de Vitòria? Fem llavors l'equip d'Euskadi. I hi ha algú més? Bé, fem un equip mundial. Però ara ens sorgeix un gran problema. En un grup de WhatsApp a nivell mundial, és clar que no serem capaços de llegir tots els missatges i encara serà més difícil comprovar totes les transaccions (missatges): no sabrem a qui deu, ni en quina ordre s'han realitzat les transaccions (no és el mateix gastar després de rebre els diners que gastar primer els diners i després rebre els diners, que no és legal). Per això, en un gran compte és imprescindible unir les transaccions en una quantitat fixa creant blocs[5]. Per tant, cada missatge de WhatsApp serà un conjunt de transaccions.
Tanmateix, podem pensar que això no soluciona el problema, ja que ara en lloc d'un munt de transaccions tenim un munt de blocs. Si cada usuari crea un bloc no solucionarem el problema. Per això, ha de ser difícil crear un bloc per a un usuari, però senzill per a altres usuaris saber si el bloc està ben creat. Com podem fer-ho?
Funcions Hash
Les funcions Hash[4] són funcions molt útils per a convertir un conjunt de dades en dades de grandària coneguda.
hash = hashfunción (missatge)
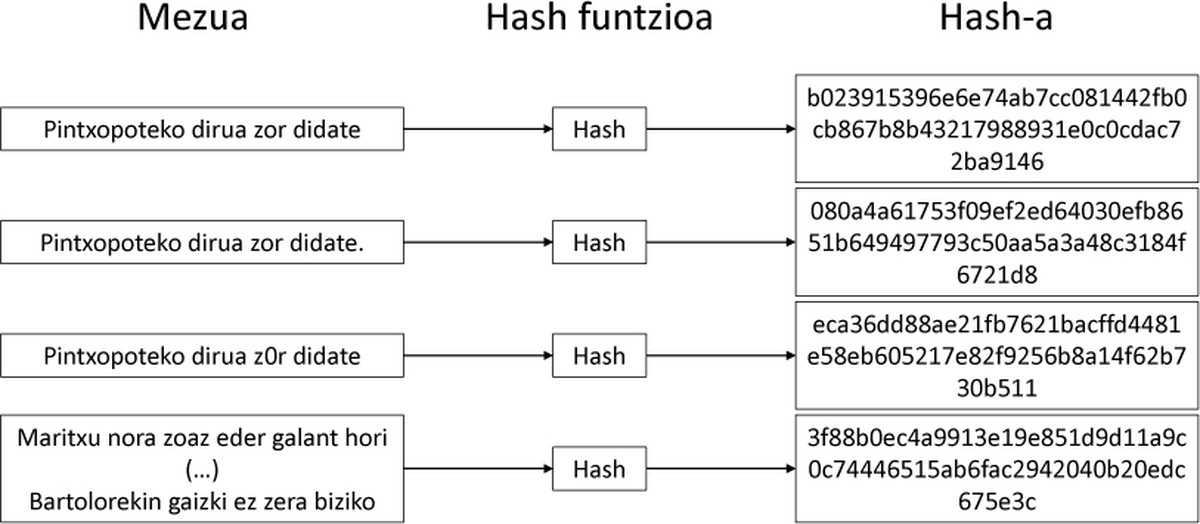
No obstant això, les funcions Hash tenen una propietat molt especial: si canviem una mica el missatge, la sortida variarà molt. El canvi és tan gran que ens sembla aleatori la sortida de dos missatges molt similars. En la figura 2 es mostra un exemple clar.
Per tant, si a nosaltres ens donen un missatge, és molt fàcil aconseguir el seu hash, però amb l'hash no podrem saber quin era el missatge original. L'única manera d'aconseguir-ho és a través d'assajos, canviant el missatge fins a aconseguir l'hash desitjat.
I com ens pot ajudar? Un bloc (un conjunt de transaccions) és només un missatge. Així, podem trobar l'hash del bloc, tenint sempre en compte que l'hash del nostre bloc variarà en funció del contingut i ordre de les transaccions.
Ara escriurem alguna cosa al final del bloc, un conjunt de caràcters. Però, per què?
Proof-of-work
Es posarà una restricció als blocs: l'hash del bloc ha de tenir diversos 0 al principi. Per a aconseguir-ho, tal com s'ha indicat anteriorment, al final del bloc escriurem un conjunt de caràcters anomenat nombre màgic. Com hem dit, no és possible tornar de l'hash al missatge, ja que l'única manera d'obtenir els 0 és intentar moltes combinacions de caràcters fins a aconseguir la quantitat 0 desitjada. Aquest càlcul consumeix molts recursos de l'ordinador (temps i electricitat). Això vol dir que si un bloc té un hash de molts 0, algú ha gastat molta energia a calcular-la, per la qual cosa és un bloc fiable.
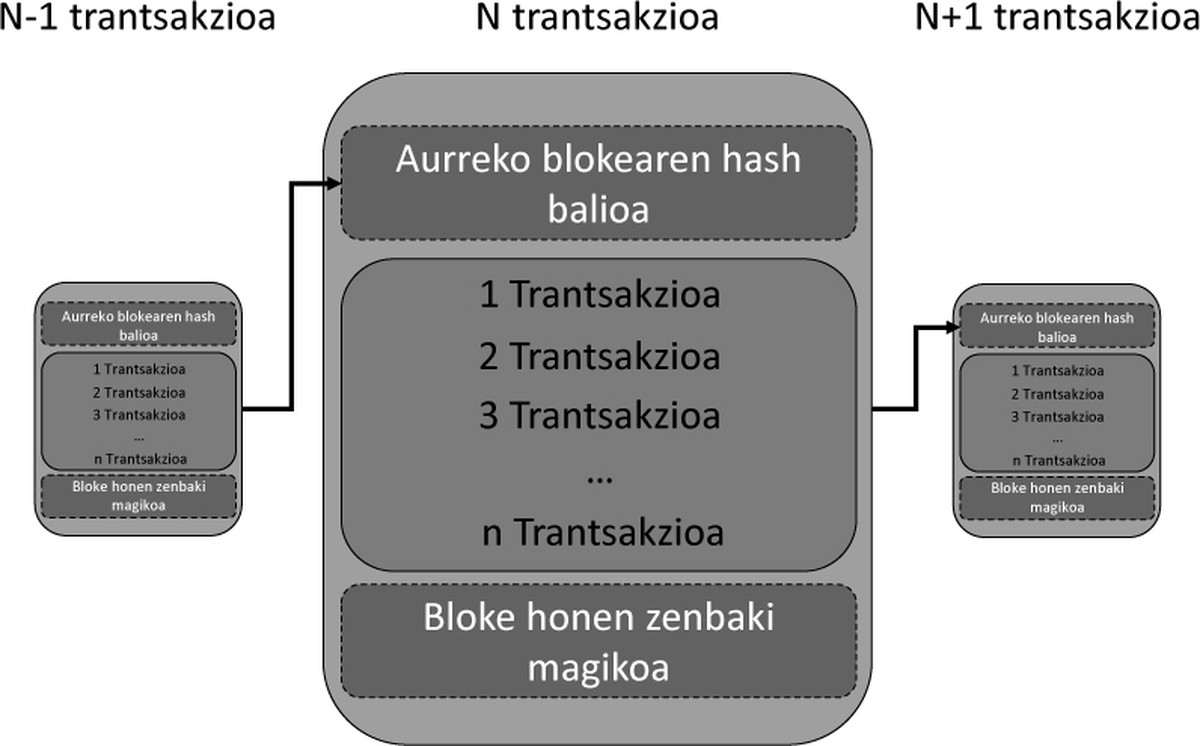
Com hem dit, és fàcil comprovar si es compleix la regla de l'hash. Per això, no té sentit intentar fer paranys, ja que els atraparien amb facilitat. Però, per què la gent ho faria? Per què fer tots aquests càlculs per a calcular l'hash del bloc? La resposta és senzilla, perquè hi ha un premi per a qui primer crea el bloc. Aquest premi no és més que un valor dins del compte: en l'exemple de la quadrilla el menjar o beguda per al poteo de pintxos, en el cas de la vitcoina les bitcoinas. Aquest procés es denomina mineria. El bloc es completa amb l'hash del bloc anterior. Així els blocs estan ordenats. En la figura 3 es mostra l'estructura del bloc.
Relació entre cadenes de blocs i bitcoina
Però, llavors, com es relacionen l'estructura que hem descrit (cadenes de blocs) amb la criptomoneta més famosa del món? Això de les cadenes de blocs és només un concepte, una manera de portar comptes. Moneda de les cadenes de blocs Bitcoina, moneda electrònica per a portar comptes utilitzant cadenes de blocs. De la mateixa manera, la suma és només un concepte matemàtic i una expressió de 5+2 "".
Conclusions
Encara que més desconeguda, en aquest article s'ha atribuït a les cadenes de blocs un èmfasi major que a la vitcoina. Per què? Doncs perquè a més de la vitcoina hi ha moltes altres criptomonetas (ethereum, litecoin, dash..), però totes són expressions del mateix concepte: de les cadenes de blocs. Les criptomonetas poden pujar o baixar en el mercat, poden crear-se i desaparèixer. En qualsevol cas, és clar que les cadenes de blocs estaran presents en la nostra vida en els pròxims anys en les criptomonetas per a compartir informació o, potser, per a evitar problemes de pintxo-poteo.
Referències
[1] Whitfield Diffie and Martin Hellman. New directions in cryptography. En: IEEE transactions on Information Theory 22.6 (1976), pàg. 644–654.
[2] Fileformat.info: Hash functions. https :// www . fileformat . info / tool/hash.htm
[3] Satoshi Nakamoto. Bitcoin: A Peer-to-Peer Electronic Cash System. Novembre 2008. 2015
[4] Bart Preneel. “The first 30 years of cryptographic hash functions and the NIST SHA-3 competition”. En: Cryptographers’ track at the RSA conference. Springer. 2010, pàg. 1–14.
[5] Melanie Swan. Blockchain: Blueprint for a new economy. "O’Reilly Em- dia, Inc.", 2015
[6] Youtube channel 3Blue1Brown: Ever wonder how Bitcoin (and other cryptocurrencies) actually work? https://www.youtube.com/watch? v=bbc-nXj3Ng4.





