Pintxo-pote kontuak, blockchaina eta bitcoina

IMDEA Networks Institutua (Madril); Carlos III Unibertsitatea (Madril)

Zabaldu:
Twitter
Facebook
Emaila

Asko entzun izan dugu azken urte hauetan blockchainari eta bitcoinari buruz. Baina zer dira? Posible al da ulertzea nola funtzionatzen duten, eguneroko adibide sinple batekin? Hori da, hain zuzen ere, artikulu honen helburua; izan ere, blockchain edo bloke-kate kontzeptua alderatuko dugu Euskal Herrian aurrez aurre izan ohi dugun arazo batekin: nola egin diru-kontuak lagunekin pintxo-poteora zoaztenean.

Interneten onurak ukaezinak dira. Lehen aldiz gizarte osoa konektatzen duen tresna bat dugu eskura. Dena den, konexio horrek paradigma berri bat sortu du. Erabiltzaileok ezin dugu jakin sarearen beste aldean dagoen pertsona fidagarria ote den. Beraz, nola lor dezakegu guztiok elkarren artean informazioa partekatzea inork inoren identitatea ordeztu eta informazio pribatua aldatu gabe?

Azken urteetan arazo hori konpontzeko aurkitu den konponbide ezagunena aztertuko da artikulu honetan, betiere lagunekin diru-kontuak egitea adibidetzat hartuz: blockchaina edo bloke-kateak[3][6], alegia. Horretarako, lehenik eta behin, bloke-kateak zer diren ulertzeko ezinbestekoak diren hainbat kontzeptu azalduko dira, baita zer onura eta arazo ekar ditzaketen ere.

Zer dira bloke-kateak?

Imajina dezagun lagunekin gaudela, adibidez, Donostiako Gros auzoko pintxo-potean. Nola ordainduko ditugu gure pintxo-poteak? Alde batetik, posible da bakoitzak berea ordaintzea, baina argi dago ez dela aukerarik efizienteena, denbora asko beharko baikenuke ordaintzeko. Beste aukera bat litzateke denen artean poto bat jartzea, horrela askoz ere azkarrago ordainduko baikenuke. Alabaina, horrek beste arazo batzuk dakartza: zer gertatuko litzateke potoko dirua nahikoa ez balitz? Eta soberan badago amaieran? Askotan prezio guztiak ez dira berdinak izaten, kasu horretan, nola banatuko genuke ordaindu beharrekoa?

Arazo horiek ikusita, beste konponbide egokiago batean pentsa dezakegu. Sor dezagun kontu bat, non kide bakoitzak jarriko duen taberna bakoitzean zenbat zor duen eta nori zor dion. Kontu hori ahalik eta gardenena izateko, paper batean idatzia egon ordez, datu guztiak online egongo dira denek ikusi ahal ditzaten, adibidez WhatsApp talde batean. Baina zer gertatuko litzateke taldekideak fidagarriak ez balira? Ikus dezagun zer trikimailu erabil ditzakegun fidagarritasun-arazo hori konpontzeko. Azken finean, bloke-katea hori besterik ez da: partaide orok elkarren arteko transakzioak idazteko erabil dezakeen kontu erraldoi bat. Ikus dezagun, beraz, zer den transakzio bat.

Transakzioa

Esan bezala, kontuan agertuko da pertsona bakoitzak taberna bakoitzean zenbat eta nori zor dion. Bi modu daude hori egiteko: ordaindu duenak idaztea kontuan edo zor duenak idaztea. Argi dago lehen aukera ez dela komenigarria, partaideren bat diru faltan balego beste batzuek zor diotela jarri bailezake kontuan. Beraz, zorduna izango da idatziko duena zenbat diru eta nori zor dion. Hala, ziurtatuko dugu inork ez duela tranparik egingo, kontuan zerbait idaztean dirua galdu egiten da eta. Horri bloke-kateetan transakzio deritzo. Baina nola jakin dezakegu pertsona hori benetan gai den idatzi duen zenbatekoa ordaintzeko? Oso erraz. Transakzio bat idazten den bakoitzean, kontu horretan (kasu honetan, WhatsApp taldean) dagoen pertsona bakoitzak egiaztatu behar du ea zordunak nahikoa moneta duen transakzioa ordaintzeko. Hala ez bada, transakzioa bertan behera uzten da. Eta nola jakin dezakegu nahikoa duen? Erraz, aurreko transakzio guztiei begiratuz jakin baitezakegu ea zorra kitatzeko nahikoa duen. Puntu honetan jada atzeman dezakegu non dagoen kontuaren (gure kasuan WhatsApp taldearen) balioa: aurretik zor didaten pintxo-poteko zenbatekoa erabil dezakegu pintxo-pote berri batean. Dena den, nola ziurta dezakegu nire transakzioak nik bakarrik idazten ditudala?

Sinadura digitala

Sinadura digitala[1] arazo bakar bat konpontzeko sortu zen: mezu baten jatorria egiaztatzea. Nahiz eta gizakiok mezu bat hizki-multzo baten gisara ikusi, ordenagailu batek bit-multzo gisara ikusten du mezu bat (edozein artxibo, egia esan).

Suposa dezagun erabiltzaile asko ditugula. Sinadura digitalak sortzeko algoritmoak bi dira: lehena sinadura sortzeko erabiltzen da, eta bigarrena, sinadura egiaztatzeko. Erabiltzaile bakoitzak giltza deituriko bi kode ditu, bata pribatua (G_pr) eta bestea publikoa (G_pu). Sinadura sortzeko funtzioa honako hau da:

sinadura = sinadurasortu(mezua, G_pr)

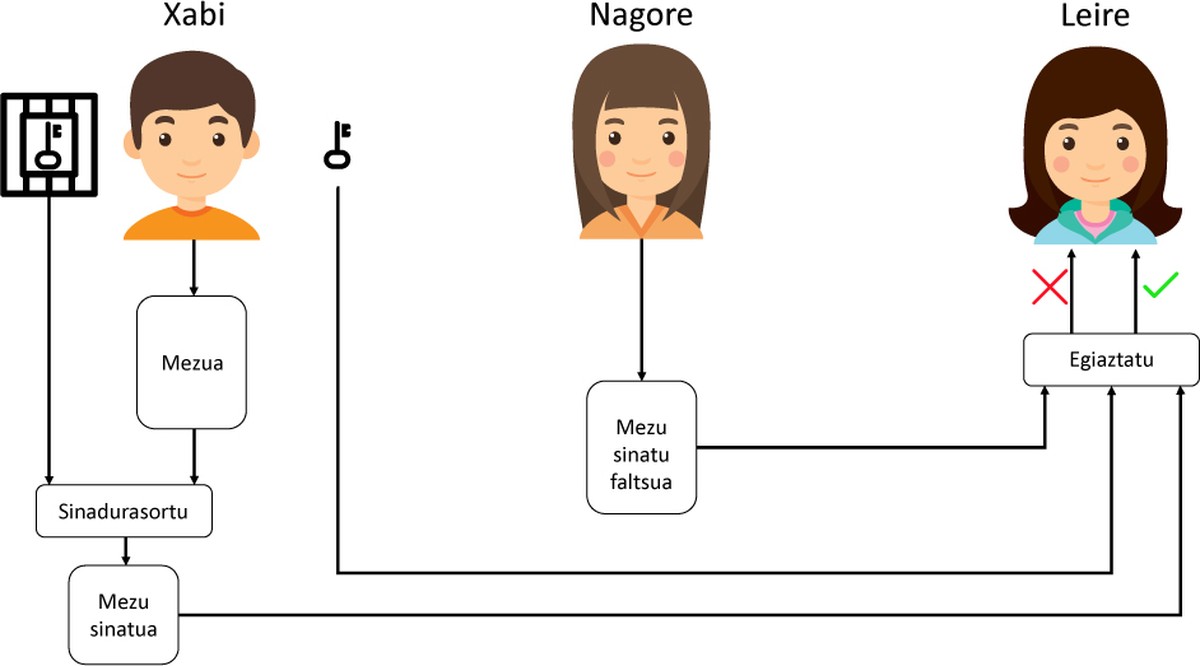
1. irudia: Leire Xabiren mezu baten zain dago. Nagorek mezua bidali nahi dio Leireri Xabiren izenean, Leire engainatzeko. Dena den, Xabik bere mezu eta giltza pribatuarekin sinatu du mezua. Leirek, orduan, sinadura publikoarekin egiaztatu ditu jasotako bi sinadurak, eta Xabirena identifikatu du, eta Nagorerena baztertu. Arg. Ander Galisteo

Hemen hautematen dugu pertsonen sinaduraren eta sinadura digitalaren arteko alde nabariena. Ikus daitekeen moduan, sinadura bakoitza mezu eta erabiltzaile bakoitzarentzat sortzen da; beraz, sinadura digitala mezuaren eta erabiltzailearen araberakoa izango da (pertsonek sinadura bera erabiltzen dugu dokumentu guztiak sinatzeko). Horrek esan nahi du, besteak beste, gure G_pr-a mezu ezberdinetan erabil dezakegula behin eta berriro, segurtasunik galdu gabe.

Bestetik, sinadura egiaztatzeko beste funtzio bat ere badugu:

bai/ez = egiaztatu(mezua, G_pu, sinadura)

Funtzio horrek sinaduraren jatorria zein den esaten digu, sinadura, mezua eta giltza publikoa erabiliz. Modu erraz horren bidez jakin dezakegu mezua benetan nahi dugun erabiltzaileak bidali duen. Adibide gisa, ikusi 1. irudia.

Blokea

Orain arte esan duguna erabilgarria izango litzateke kuadrilla txiki batean, eta arazo handirik gabe aplikatu ahal izango litzateke. Baina, normalean, pintxo-poteoan ez gara kuadrillarekin bakarrik egoten; gehienetan, kirol-taldekoekin, unibertsitatekoekin, dantza-taldeko kideekin... topatzen gara, eta, kasu horretan, kuadrillarekin egindako kontuak ez digu balio. Egin dezagun, orduan, Donostiako WhatsApp taldea, donostiar guztiak barnean hartuko dituen taldea. Eta Gasteizko norbait badago? Egin dezagun, orduan, Euskadiko taldea. Eta kanpoko beste norbait badago? Ondo da, egin dezagun mundu mailako taldea. Baina, orain, arazo handi bat sortzen zaigu. Mundu mailako WhatsApp talde batean, argi dago ez garela gai izango mezu guztiak irakurtzeko, eta oraindik zailagoa izango da transakzio (mezu) guztiak egiaztatzea: ez dugu jakingo nork nori zenbat zor dion, ezta transakzioak zer ordenatan egin diren ere (ez da gauza bera dirua jaso eta gero gastatzea, edo lehenik dirua gastatu eta ondoren dirua jasotzea, azken hori ez baita legezkoa). Horregatik, kontu handi batean ezinbestekoa da transakzioak kantitate finko batean elkarrekin jartzea, blokeak[5] sortuz. Beraz, WhatsAppeko mezu bakoitza transakzio multzo bat izango da.

Dena den, pentsa dezakegu horrek ez duela arazoa konpontzen, orain transakzio-mordo baten ordez bloke-mordoa baitugu. Erabiltzaile bakoitzak bloke bat sortzen badu, ez dugu arazoa konponduko. Horregatik, zaila izan behar du erabiltzaile batentzat blokea sortzea, baina erraza beste erabiltzaileentzat, blokea ondo sortua dagoen jakitea. Nola egin dezakegu hori?

Hash funtzioak

Hash funtzioak[4] oso funtzio erabilgarriak dira, datu-multzo bat tamaina ezaguneko datu bihurtzeko.

hash = hashfuntzioa(mezua)

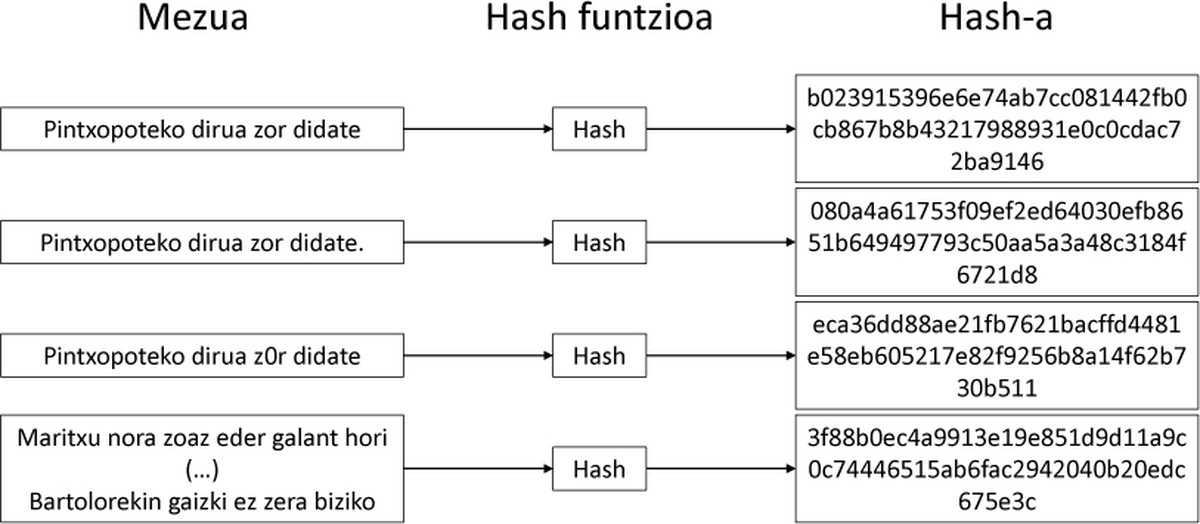
2. irudia: Hash funtzioaren zenbait adibide[2]. Lehen, bigarren eta hirugarren adibideetan ikus daitekeenez, aldaketa oso txikia egitean oso hash ezberdina sortzen da. Bestetik, kontuan eduki behar dugu berdin duela mezuaren luzera zein den (laugarren adibidean, Maritxu nora zoaz abesti osoa erabili da hash-a sortzeko), hash-aren luzera beti tamaina berekoa izango baita.

Hash funtzioek, ordea, propietate oso berezi bat dute: mezua pixka bat aldatzen badugu, irteera asko aldatuko da. Hain da handia aldaketa, ezen ausazkoa iruditzen baitzaigu oso antzekoak diren bi mezuren irteera. Adibide argia ageri da 2. irudian.

Beraz, guri mezu bat ematen badigute, oso erraza da haren hash-a lortzea; baina hash-a emanda, ezingo dugu jakin jatorrizko mezua zein zen. Hori lortzeko modu bakarra saiakerak egitea da, mezua aldatuz nahi dugun hash-a lortu arte.

Eta nola lagundu gaitzake horrek? Bloke bat (transakzio-multzo bat) mezu bat besterik ez da. Hala, blokearen hash-a aurkitu dezakegu, betiere kontuan edukiz gure blokearen hash-a ezberdina izango dela transakzioen eduki eta ordenaren arabera.

Orain, blokearen amaieran zerbait idatziko dugu, karaktere-multzo bat hain zuzen ere. Baina, zergatik?

Proof-of-work

Murrizketa bat jarriko diegu blokeei: blokearen hash-ak hainbat 0 izan behar ditu hasieran. Hori lortzeko, lehen esan bezala blokearen amaieran karaktere-multzo bat idatziko dugu, zenbaki magikoa deiturikoa. Esan bezala, ez da posible hash-etik mezura bueltatzea, 0ak lortzeko modu bakarra baita karaktere konbinazio asko saiatzea, nahi dugun 0 kopurua lortu arte. Kalkulu horrek ordenagailuaren baliabide asko kontsumitzen ditu (denbora eta elektrizitatea). Horrek esan nahi du bloke batek 0 askoko hash-a badu norbaitek energia handia xahutu duela hori kalkulatzen, eta, beraz, bloke fidagarria dela.

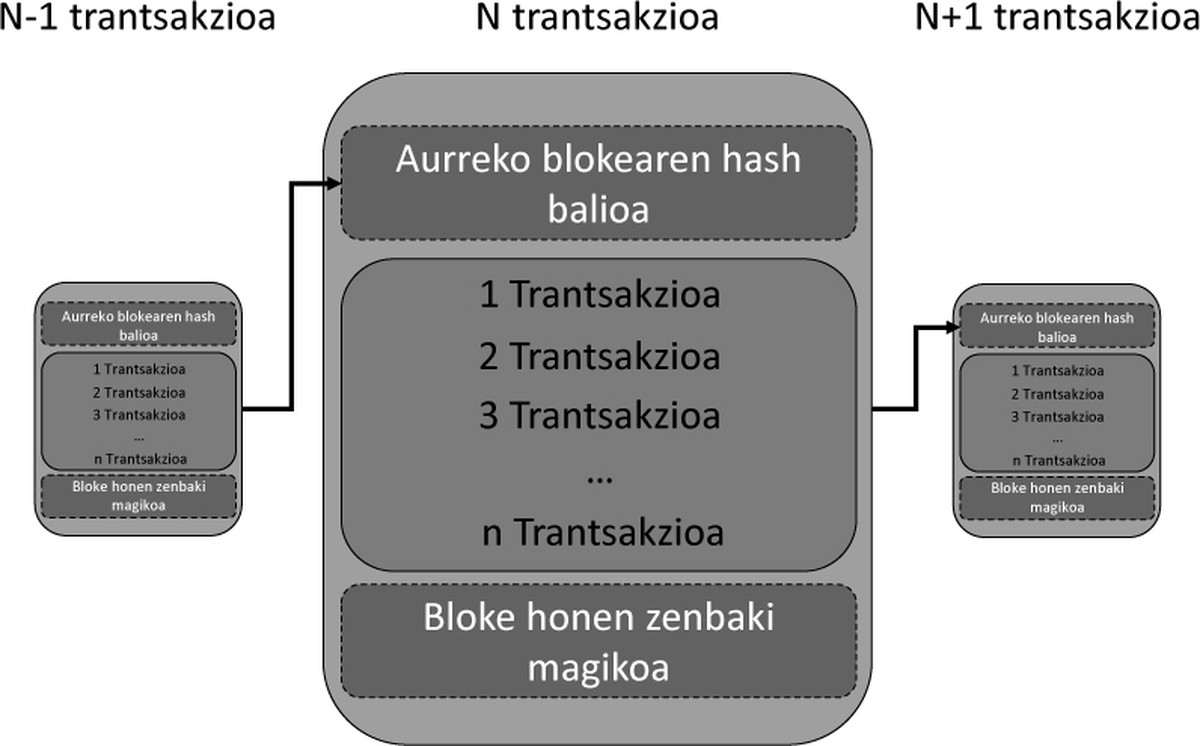
3. irudia: Blokeak hiru zatitan banatzen da. Lehena, aurreko blokearen hash-a da; honela bloke guztiak ordenan daude. Bigarrena, blokearen transakzioak dira. Azkena, zenbaki magikoa da: hash-a 0ekin hasteko erabiltzen dena. Arg. Ander Galisteo

Esan bezala, erraza da hash-aren araua betetzen den ikustea. Hori dela eta, ez du zentzurik tranpa egiten saiatzea, oso erraz harrapatuko bailituzkete. Baina, zergatik egingo luke jendeak hori? Zergatik egin kalkulu horiek guztiak blokearen hash-a kalkulatzeko? Erantzuna sinplea da: sari bat dagoelako blokea lehenik sortzen duenarentzat. Sari hori kontuaren barruko balioa besterik ez da: kuadrillaren adibidean pintxo-poteorako jana edo edaria, bitcoinaren kasuan bitcoinak. Prozesu horri meatzaritza deritzo. Blokea osatzeko, aurreko blokearen hash-a jartzen da. Honela blokeak ordenaturik daude. 3. irudian ikusten dugu blokearen egitura zein den.

Bloke-kateen eta bitcoinaren arteko erlazioa

Baina, orduan, nola erlazionatzen dira azaldu dugun egitura (bloke-kateak) eta munduko kriptomoneta famatuena? Bloke-kateena kontzeptu bat besterik ez da, kontuak eramateko modu bat. Bitcoina bloke-kateen moneta, bloke-kateak erabiliz kontuak eramateko moneta elektronikoa. Modu berean, batuketa kontzeptu matematiko bat baino ez da, eta "5+2"-ren adierazpen bat.

Ondorioak

Nahiz eta ezezagunagoa izan, artikulu honetan bloke-kateei bitcoinari baino enfasi handiagoa eman zaie. Zer dela eta? Bada, bitcoinaz gainera beste kriptomoneta asko daudelako (ethereum, litecoin, dash...), baina denak kontzeptu beraren adierazpenak dira: bloke-kateenak. Kriptomonetak igo edo jaitsi egin daitezke merkatuan; sortu eta desagertu daitezke. Nolanahi ere, argi dago bloke-kateak gure bizitzan egongo direla datozen urteetan, kriptomonetatan, informazioa partekatzeko edo, agian, pintxo-poteoko arazoak ekiditeko.

Erreferentziak

[1] Whitfield Diffie and Martin Hellman. “New directions in cryptography”. In: IEEE transactions on Information Theory 22.6 (1976), pp. 644–654.

[2] FileFormat.info: Hash functions. https :// www . fileformat . info / tool/hash.htm.

[3] Satoshi Nakamoto. Bitcoin: A Peer-to-Peer Electronic Cash System. November 2008. 2015.

[4] Bart Preneel. “The first 30 years of cryptographic hash functions and the NIST SHA-3 competition”. In: Cryptographers’ track at the RSA conference. Springer. 2010, pp. 1–14.

[5] Melanie Swan. Blockchain: Blueprint for a new economy. " O’Reilly Me- dia, Inc.", 2015.

[6] Youtube channel 3Blue1Brown: Ever wonder how Bitcoin (and other cryptocurrencies) actually work? https://www.youtube.com/watch? v=bBC-nXj3Ng4.