Hasiera »   Gai librean »   Karga-banaketa zerbitzari-multzoetan

Load sharing in server groups

• Zabaldu:
• Twitter
• Facebook
• Emaila

The distribution of cargo in current computer systems has become a very important issue. The complexity and gigantic nature of these systems means that their behaviour cannot be managed centrally. Therefore, we will present a decentralized model based on selfish routers and, using game theory, we will contrast its behavior with the optimal solution. We will show that the model based on selfish routers is very close to the optimal solution. Finally, we will indicate how companies like Google or Facebook can use our result.

Telecommunications networks have increased considerably in recent decades. On the other hand, its complexity increases as new technologies develop. Therefore, telecommunications networks cannot be managed centrally. For example, Google is considered to have more than a million servers spread across different countries, demonstrating the impossibility of centralized management. Therefore, we can affirm that the management of computer systems is based on distributed systems. Therefore, many researchers are currently working on this issue: Does the behavior of distributed systems change much with respect to the centralized system?

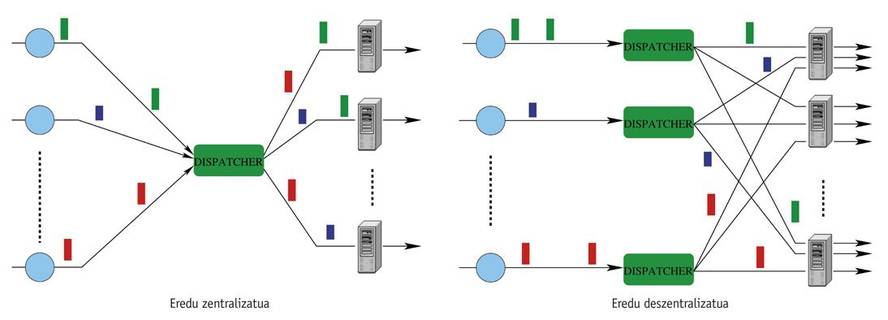
The mathematical model of load distribution in server groups is presented, responding to the question in the previous paragraph. To do this, we will compare two models of load distribution: in the centralized model, on the one hand, the distribution of all customer orders is carried out by a single router; on the other hand, the decentralized model consists of several routers and each of them takes care of a part of all orders.

This comparison will be made thinking that the routers of the decentralized model are selfish. The selfish router aims to reduce the service time of incoming requests. Therefore, each selfish router aims to solve a different optimization problem. In addition, the characteristics of these optimization problems allow us to define a game between the routers themselves. That is, taking into account selfish routers we can use results based on game theory.

But what is game theory? Game theory is the field of mathematics that aims to analyze individual strategic behaviors. The fact that telecommunications networks are distributed systems shows that game theory is a good model of computer system design and research, which has made many telecom network researchers interested in game theory in recent years.

We have defined a competitive game in the decentralized load distribution model, in which each router can decide to send loads to each server to reduce the service time of their requests. The competitive gaming solution is called Nash Oreka. In our model, Nash Oreka is the solution of the game. The cost of anarchy (CMI) is used to measure the distributed performance of computer systems.

The cost of anarchy is the division between the worst behavior of the Nash Balance and the behavior of the optimal solution. Several researchers have investigated load distribution CDs in recent years. According to the literature, the cost of anarchy has in some cases enormous values, so it can be concluded that the behavior between the centralized and the decentralized model can be very different. We have shown that the cost of anarchy is not an adequate measure to compare the behavior of the centralized and decentralized model of balance load. In fact, although the value of the IMT is high, we will see that both models have similar behavior.

The characteristics of a group of servers have been fixed and all other system parameters have been modified, choosing among them most of the behaviors of both models, that is, the value of the inefficiency of this group of servers. If it is shown that the inefficiency of a set of servers is low, it can be concluded for this group of servers that there are no behavioral differences between both models.

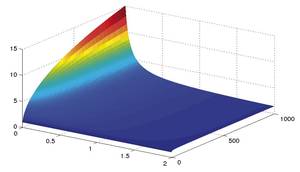
It has been calculated when the worst case of inefficiency occurs among all server groups, that is, in which cases the cost of anarchy appears. Therefore, when there is a fast server and the speed difference between the fast and inert server is huge, we have obtained the value of the cost of anarchy. In all other server groups it has been observed that the value of inefficiency is low.

We know that in the giant sets of servers the value of the CMI is very high. Depending on the result obtained, although the value of the CMI is very high, it is observed that the value of the inefficiency of a set of servers (that is, the difference between the behaviors of the centralized and decentralized model of a set of servers) is very low in all server groups, except in one case.

We believe that our results have a practical application. Companies like Google, Facebook or Amazon use a large number of servers to serve their customers. Since the centralized solution is not always implementable, the decentralized model based on selfish routers is a good opportunity for these companies. Our results indicate that if Facebook and Google use selfish routers, their behavior will be close to the optimal solution of the load distribution problem.

References

Thank you

P. Authors Brun (LAAS-CNRS), B. Prabhu (LAAS-CNRS) and U. Ayesta (LAAS-CNRS and IKERBASQUE-UPV/EHU) thanks the technical assistance provided.