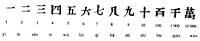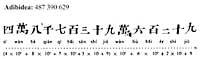Historia das cifras (III)
Avanzando

Os sistemas numéricos iniciais baseábanse no principio aditivo, é dicir, repetíanse tantas veces como sexa necesario paira representar un número (símbolos). Por exemplo, o número 2619, nalgúns sistemas, necesitaría dezaoito símbolos. Estes sistemas non cubrían as necesidades dos contables. Por iso, desde a época do antigo Imperio (a. C.) XXVIII - XXIII. séculos) os escribanos egyptianos trataron de facilitar a escritura até conseguir a chamada numeración hierática
...
As novas formas das cifras apenas lembraban as iniciais. Paira escribir o número 2619 só debían escribir os símbolos correspondentes aos números 2000, 600, 10 e 9.
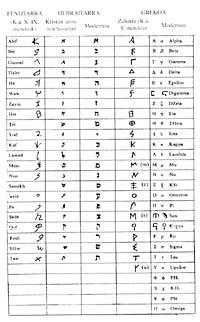
Dous mil anos despois, aos escribanos israelís e aos matemáticos gregos ocorréuselles o mesmo, pero esta vez, sen esquematizar os símbolos, os números fóronse adaptando as letras do alfabeto.
Alfabeto A.C. Cara ao ano 1.500 os fenicios inventaron Syria na costa palestina. En Oriente foi transmitida aos pobos de Moa?a, edomar, ammonar e hebreo. Tamén aos nómades arameses, que en Oriente Próximo dispersárono desde Egypto até a India. a.C. IX. A partir do século XX estendeuse polo Mediterráneo, sendo aprobada polos pobos occidentais de forma progresiva.
Vinte e seis letras fenicias crearon a escritura paleo-hebraica e arameana (da que derivaron alfabeto palminio, nabatar, syriar, árabe, persa, turco e hindú). Tamén foi a base do alfabeto grego. Grego é o primeiro alfabeto que introduciu a escritura estrita das vocais. Este último foi suxestivo do alfabeto etrusco, máis tarde latino, e máis tarde do gótico, xeorxiano, armenio e quirílico. Cabe destacar que todos os costumes conservaron durante séculos os nomes e a orde das vinte e seis letras.
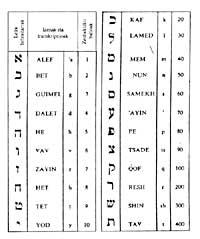
Os hebraitarras escribían as letras paira escribir os números, empezando pola dereita á esquerda e a máis grande. Entre os dous últimos símbolos paira separar os números das palabras escribíanse dúas comiñas e cando a cifra era única, na parte superior esquerda só una comilla.
Pero o número máximo que podían escribir con este método era catrocentos. A pesar de buscar solucións, non conseguiron grandes avances. Facilitaron a escritura até o número 999.999 e a partir de aí os obstáculos non desapareceron.
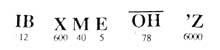
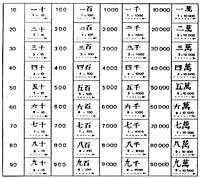
Aos aritméticos gregos tamén se lles ocorreu que representasen os números en letras. Ao alfabeto clásico engadíronselle os signos digamma, san e qopp a.
Os números intermedios escribíanse con letras xuntas. Paira distinguir entre palabras e números dentro dun texto, estes rematábanse cunha liña horizontal. Escribían una comilla na parte superior e esquerda das letras da unidade de escribir números de 1.000 a 9.000.
Non sabemos cal destes dous sistemas é o máis antigo, entre o hebreo e o grego. Os máis antigos son os gregos, papiros de Elefantina (a. C.) 331-330) e moedas de Ptolomeo II Filadelfio (a.C.) 286-246). Os hebranos, pola súa banda, son as moedas da dinastía asmonear as máis antigas; a. C. 78. Con todo, isto non significa nada de antigüidade.
A principal vantaxe desta escritura alfabética foi o resumo da escritura. O número 479 escribíase en tres cifras (letras). Con todo, a maioría dos países mencionados seguiron utilizando o principio aditivo. Por tanto, os recursos da súa numeración escrita seguiron sendo limitados.
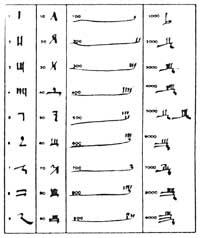
O pobo que buscaba outra solución diferente foi o chinés. Estes tiñan trece símbolos especiais.
En realidade os símbolos non son cifras, senón imaxes normais da escritura chinesa. Indican non só o valor gráfico, senón tamén o valor fonético que corresponde aos nomes dos números chineses. Aínda que hoxe en día os distintos símbolos utilízanse en función da notación chinesa, tamén se pronuncian. As grafías da figura anterior son do tipo kaish-ou, o máis estendido hoxe, o máis simple e o máis antigo dos contemporáneos (IV. Mantense como se utilizaba no século XIX).
Outra forma que utilizan é o guàn zi (cifras oficiais). É máis complicado que o anterior, utilízase en papeis oficiais e xorde paira evitar fraudes. A terceira forma, denominada xíngshu, xorde paira resumir e acelerar a escritura. Utilízase en escribanos, bosquexos, etc. Co exceso de abreviaturas, os símbolos anteriores convertéronse nunha grafía excesivamente resumida chamada caoshu, que só os expertos entendían. Por último temos cifras denominadas ngán mà ou gán mà zí (marcas secretas), utilizadas en criptografía. Tamén os utilizan os comerciantes.
En todas as formas utilízase o mesmo principio de numeración paira expresar os números. Os múltiplos da décima escríbense utilizando o principio de multiplicación e os números intermedios combinan os principios de multiplicación e suma. Este principio tivo dúas vantaxes principais: os símbolos non se repetían tantas veces e na memoria había que gardar menos símbolos diferentes. Grazas a iso conseguiron escribir grandes números con poucos símbolos (do 1 ao 999 999 999 999 999 999 999 999). Con todo, este método non facilitaba o cálculo das operacións, que se realizaban en ábaco, táboa, regra, ...