1988/04/01 14. zenbakia

eu es fr en cat gl

• Itzulpen automatikoa
  • Español
  • Français
  • English
  • Català
  • Galego
  • Jatorrizkora itzuli

Elia Elhuyar

×

Aparecerá un contenido traducido automáticamente. ¿Deseas continuar?

Si No

Elia Elhuyar

×

Un contenu traduit automatiquement apparaîtra. Voulez-vous continuer?

Oui No

Elia Elhuyar

×

An automatically translated content item will be displayed. Do you want to continue?

Yes No

Elia Elhuyar

×

Apareixerà un contingut traduït automàticament. Vols continuar?

Si No

Elia Elhuyar

×

Aparecerá un contido traducido automaticamente. ¿Desexas continuar?

Se No

• Programazioa

Cyclist distribution cyclist

• Zabaldu:
• Twitter
• Facebook
• Emaila

Due to the turns of the cyclists, many times we take this opportunity to bet between friends.

Each participant is randomly assigned several cyclists, winning or losing according to what they do.

Here is a possible bet:

To the winner of the stage, each one will give him a hard one. This bet is made daily.
• Winner of the return (once finished) 50 ptas. Each one. He will deliver them. The second, 25 ptas. each and the third, 10 ptas.

To the winner of intermediate destinations, each 10 ptas. delivery (once complete return is finished).

To the winner of mountain ports, each 25 ptas. delivery (once complete return is finished).

To the winner of the team classification, each 25 sts. delivery (once complete return is finished).

This is a program that will help you to avoid cyclists.

Observations:

1.- In the previous number we analyzed the problem of repetition of random. On this occasion, we should randomly order a set of numbers (corresponding to cyclists). Therefore, two conditions must be taken into account:

In the final list each number should only appear once. This list must contain all the numbers. To solve this problem we will follow the following steps: Once the random number is extracted, it will be used as an index of this table and the element located in the place indicated by the random will go to another table (lines 390-410). To prevent the same number from being repeated, this element must be removed from the matrix, advancing a later position. In addition, the random area should be updated by reducing one each time an element is erased (lines 420-440). Note that although the random is repeated, in the position representing this random number there will be no number that already existed. This will prevent the numbers from being repeated in the final list. On the other hand, since this process is repeated until all the elements of the first table or matrix are deleted, all the initial elements will be in the second list.

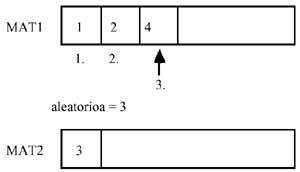
2.- In order to make the distribution as equitable as possible, the heads of the groups have been included in another table, separating the first (lines 110 to 120). It may happen that not all participants have the same number of cyclists. In these cases, the program has been drafted so that the greatest difference between participants is one participant (lines 210-270).

3.- For participants who have to stay with less cyclists not always be the same, the best solution has been to randomly order participants (lines 90-100).

4.- In this program we have not taken into account the names of the cyclists, but the numbers they carry.

5.- Enter in line 1010 all the names of those who are going to participate in the draw before running the program.

6.- Our limitations are: Number of cyclists: 200 Number of teams: 20 Assistants: 20 If you want to overcome these limits you will need to modify the dimensions of the matrices in line 20.

10 CYCLISTS REM 20 DIM TXIRRIN1(20),TXIRRIN2(200),PARTICIPANT(20), MAT1(200),MAT2(200) 30 KEY OFF : SCREEN 2,0 : CLS 40 LOCATE 3,28:PRINT "CYCLISTS DISTRIBUTION": LOCATE 4,28:PRINT "=======================" 50 LOCATE 10,10: INPUT "Total number of cyclists";KOP1 60 LOCATE 12,10: INPUT "How many teams are";EKI 70 LOCATE 14.10: NUM.1(Number of participants)