Supercordes, révolution ou rêve ?
Selon cette théorie, qui a attiré l'attention de tant de prix Nobel, les fractions ne seraient pas des points minuscules, mais des cordes vibrantes. De plus, notre Univers aurait quatre dimensions non et dix : les trois spatiales, le temporel et six autres que nous ne voyons pas. Que mangez-vous! D'où allons-nous avec tout cela ?
De temps en temps surgissent des théories qui remettent en question nos croyances antérieures et créent des visions révolutionnaires de nouveaux points de vue. La plupart d'entre elles oublient le silence, peu d'autres concurrencent et seules certaines d'entre elles sont acceptées par tous.
Les théories des supercordes ont également réussi à attirer l'attention des scientifiques les plus prestigieux et à apprendre dans les meilleures universités il ya cinq ans. Jusqu'à présent, ils n'ont été qu'un rêve beau et désirable, mais un jour ils pourraient devenir une révolution. Par conséquent, il est préférable d'être informé.
Évolution historique
La première apparition des cordes fut un échec. En 1968, avant l’apparition de la théorie des quarks, les scientifiques étaient préoccupés par le comportement des hadrons (voir Fractions de base : le noyau de la matière Elhuyar Z. et T. Nº 55. janvier 1992). Sokena était une théorie proposée pour expliquer ce comportement. Selon cela, les hadrons n'étaient pas des fractions ponctuelles, mais des cordes tournant. Même lorsque le modèle de Quarke a prouvé sa solidité, ils ont essayé d'expliquer que les théories des cordes étaient écartées, c'est-à-dire qu'elles n'étaient pas toujours dans les hadrons et jamais libres (voir tableau).
Tout en vain; en 1974 la chromodynamique quantique (QCD) s'est développée et a accepté, laissant de côté les propositions sur les cordes.
Cependant, conscient que certaines sciences demandaient une fraction spéciale des théories de la corde, il a continué. Cette pièce spéciale avait les caractéristiques du graviton et a été pensé à utiliser les cordes pour expliquer la gravitation. En 1980, ils ont également appliqué une supersymétrie qui échange toutes les fractions, créant des théories sur les supercordes. La supersymétrie unit fermions et bosons qui travaillent dans la nature. Par conséquent, la théorie des supercordes ferait réalité, comme jamais, la plus grande unité des lois de la physique.
En 1986, toute la communauté scientifique (sauf quelques exceptions) s'est montrée très intéressée aux supercordes.
En quoi consiste la valeur des supercordes ?
Mécanique quantique vs relativité générale
XX. Le fait que les deux bases de la physique du XXe siècle, la théorie de la relativité et la mécanique quantique, soient utiles et incompatibles, a toujours provoqué une inquiétude chez les scientifiques.
Et c'est que les deux théories sont correctes dans les domaines d'utilisation habituelle. Les problèmes apparaissent à distance de marche, 10-35 m. D'une part, pour appliquer la mécanique quantique au champ gravitationnel, il faut reconnaître que la courbure spatio-temporelle est très petite, sinon il en résulterait d'innombrables éventres absurdes. Mais d'autre part, la mécanique quantique revendique l'incertitude de l'énergie, et comme la masse et l'énergie sont les mêmes, l'incertitude de l'énergie se matérialise par la génération spontanée de fractions imaginaires à vide.
Si la distance est inférieure à 10-35 m, l'énergie (et son incertitude) est si grande que, selon la relativité générale, des trous noirs virtuels sont créés. Et comme nous le savons, les trous noirs ont une très grande courbure. Par conséquent, nous pouvons considérer l'espace comme très courbe à ces distances, mais, comme nous l'avons dit au début, si la courbure est grande, les solutions de la mécanique quantique sont infinies absurdes.
C'est donc le XX. La contradiction de la physique du XXe siècle: tant la Théorie de la Relativité que la Mécanique Quantique sont correctes dans la plupart des applications (l'astronomie et la microélectronique locale), mais à distance une des deux théories (ou les deux) est erronée.
Les scientifiques croient qu'ils peuvent avoir une solution dans les cordes pour libérer ce nœud dur.
Cordes vibrantes
Pourquoi les estimations infinies mentionnées ci-dessus se produisent? Parce que les fractions étaient considérées comme des points, c'est-à-dire sans dimensions. Le problème est comme quand quelque chose est divisé par zéro. Les cordes, cependant, ont une dimension (longueur) dans laquelle les infinis disparaissent.
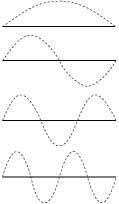
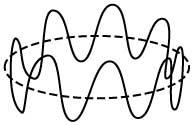
Selon la théorie des supercordes, toutes les fractions de base sont donc les sokas. En outre, une corde peut vibrer de plusieurs façons (voir figure 1). Chacun de ces états de vibration correspondrait à une fraction de masse différente. Autrement dit, la différence entre deux fractions connues est l'état de vibration. A plus d'énergie, plus de masse et d'état de vibration. D'autre part, selon les cas les plus acceptés, les cordes seraient fermées (voir figure 2).
Si oui, avez-vous dit cela que le “modèle standard” des fractions de base est faux? Pas moins. Rappelez-vous que la mécanique d'Einstein n'a pas démenti celle de Newton, mais l'a étendu, à savoir la mécanique de Newton était le cas spécial et restreint d'un autre plus général, celui d'Einstein.
La situation actuelle est la même. Les fractions « sur de grandes distances » semblent être ponctuelles, ont une activité ponctuelle et le modèle standard est parfaitement correct. À distance de marche (10-35 m), cependant, nous verrons que les fractions sont vraiment des anneaux vibrants de corde et une autre surprise.
10 dimensions
La théorie des supercordes exige que notre Univers ait 10 dimensions. La solution pour surmonter cet obstacle est la suivante: quatre dimensions (trois spatiales et temporelles) sont celles que nous percevons quotidiennement, et les six autres dimensions sont encadrées dans une petite bille. Ainsi, un point de l'espace est en fait une bille semi-dimensionnelle recueillie à 10-35 m. La mesure est si petite que nous ne pouvons pas voir d'autres dimensions.
Admettant à nouveau que l'Univers a quatre dimensions sur de grandes distances, il n'y a aucune erreur. Mais une fois descendus à 10-35 m, on noterait les 10 dimensions.
Et est-ce vrai ?
Les nouvelles conditions sont que la fraction a des cordes et que l'Univers a 10 dimensions. Qu'avons-nous gagné en retour ?
Tout d'abord, éliminer les contradictions entre la théorie de la relativité et la mécanique quantique. Deuxièmement, que toutes les fractions et forces différentes apparaissent dans un seul modèle, c'est-à-dire que toute la nature est réduite à quelques lois.
Mais pour ceux qui sont contre les cordes, en revanche, cette théorie n'a rien démontré et ne propose pas d'expériences d'affirmation. Leur caractéristique principale est leur beauté et, en dehors de cela, ils disent que ce n'est qu'une retolica des gens qui rêvent.
Ces derniers ont un peu de raison. En fait, les contributions de la théorie sont disponibles pour 10-35 m, mais l'accès à cette distance est totalement impossible avec l'instrumental actuel, c'est-à-dire qu'il n'y a aucune façon d'expérimenter.
Cependant, nous devons toujours en savoir plus sur notre monde, et si le débit est épuisé à cette théorie, nous en avons besoin. De plus, s'il était correct, nous gagnerions plus que de perdre. C'est pourquoi, en dépit de rêver, de nombreux scientifiques ont commencé à exploiter la ligne des supercordes. Le temps a la parole.
Défaite à l'origine des cordes
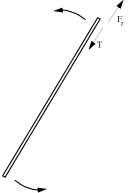
Quand les cordes sont apparues, ils ont essayé d'expliquer la structure des hadrons. Pour cela, ils disaient que les hadrons étaient des cordes tournant. Comme la corde tourne, la longueur s'allonge. Lorsque la longueur est suffisante pour que les extrémités se déplacent avec la vitesse de la lumière, la force centrifuge assimile la tension. Ce modèle, cependant, avait tort. Le modèle de quarks a été imposé et le modèle de cordes est rejeté.
Quand on a découvert que les hadrons étaient composés de quarkes, ils ont été utilisés pour expliquer le rejet des cordes. Comme nous le savons, les quarks ne peuvent pas sortir des hadrons et une auberge est créée à la chute. Les théories de la corde l'ont expliqué ainsi :
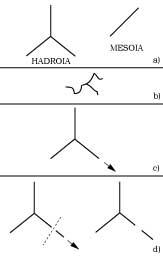
Les quarkas sont les extrémités des cordes (a), dans la taille des hadrons la force forte (identifiée avec la tension de la corde) est petite (b), mais si nous essayons de la comparer une force énorme (c) apparaît. Et si nous libérons le quarca (c.-à-briser la corde) apparaît un nouveau hadron et auberge (d). Ce deuxième modèle a également dû être écarté lorsque la chromodynamique quantique (QCD) est apparue.





