En les entranyes de la naturalesa: simetries
Zona unificada i acceleradors de fraccions

En les quatre forces bàsiques que els físics reconeixen per a explicar els fenòmens que ocorren en la naturalesa, la de la gravetat és la primera que es va crear històricament i Newton va ser el seu inventor. Mitjançant aquesta força s'estructura la relació entre les fraccions materials. En la física newtoniana, la matèria (fracció material) és l'únic element d'existència real en el marc espaciotemporal prepuesto.
No obstant això, en la dècada de 1850 Maxwell, matemàticament l'obra de Faraday, va construir una nova teoria física independent de la gravitació: Electromagnètica. En aquesta nova teoria es van definir l'Electricitat i el Magnetisme com a aspectes diferents d'un fenomen comú, com a vibracions del camp electromagnètic.
Si en la metafísica de Newton la fracció apareix com un element irreductible, la metafísica de Maxwell es basa en el camp. A partir d'aquest moment tota la ciència apareixerà submergida en la dualitat fracció/ona, i aquesta dualitat continua viva en l'actualitat.
Per a superar aquesta fracció d'identitat de la naturalesa/poder, Einstein va intentar construir la teoria de l'espai comú. Però en va. Mecànica i Electromagnetisme, obstinats, mantindran la independència entre si, apareixent la Naturalesa en les seves entranyes com a dualista (i no monista).

No obstant això, fins avui ha arribat el desig d'aconseguir la unitat de tots els àmbits, és a dir, de mostrar l'univers per una sola força. En l'actualitat, els físics, amb ajuda dels matemàtics, estan perseguint aquest objectiu amb més entusiasme que mai, i prova d'això són els gegantescos acceleradors de fraccions construïts i en construcció. Aquesta tasca no ha estat semblant en la història de la ciència, i per a construir aquestes màquines es necessiten enormes cooperacions econòmiques i socials entre els estats. (1).
Electrodinàmica quàntica
En el camí cap a un camp unificat, l'últim període de 1960-70 anys va ser molt important, ja que en aquells anys la mecànica quàntica es va adaptar amb gran èxit als camps electromagnètics. D'aquesta unió va sorgir l'electrodinàmica quàntica. Durant els quinze anys en què ha existit aquesta teoria, ha demostrat una enorme precisió i capacitat per a predir fenòmens.
Gràcies a aquest èxit incomparable, els físics van començar a quantificar altres tres forces en la naturalesa. Però de seguida van començar a resignar-se. Mentre la força violenta i la força feble no s'entenien bé, la teoria dels quarks (cromodinámica quàntica) no estava consolidada, i la gravitació escapava una vegada i una altra a la cuantización. Fa uns quinze anys la situació era la següent: Per a expressar les quatre forces que tenia en la naturalesa, hi havia quatre teories diferents, de les quals només una (l'electrodinàmica quàntica) funcionava des del punt de vista del mètode científic.
Es feia una pregunta constant sobre els investigadors. Quina era l'estructura específica del camp electromagnètic per a poder donar una representació quàntica tan adequada i precisa als altres tres camps? Si expliquem l'estructura interna del camp electromagnètic, no seria possible adaptar aquesta estructura a les altres tres zones construint així la teoria del camp unificat?
Electromagnètica i simetries de Maxwell
Des del naixement de la civilització humana, la influència dels models simètrics en el pensament i la religió és innegable, sobretot les formes simètriques. Però el concepte de simetria és molt profund i no sols compleix la simetria formal. Hi ha un camp molt ampli, encara sense explorar: la simetria més abstracta. Aquest camp de simetries abstractes ha estat la pedrera de la física moderna. I la seva importància radica en el fet que els físics d'avui creuen que l'existència de les quatre forces bàsiques que apareixen en la naturalesa es dóna per a perpetuar certes simetries que resideixen en l'estructura més senzilla de la naturalesa.
La relació entre la física i la simetria geomètrica era coneguda des de fa temps per lleis de subsistència. Les lleis de permanència ens indiquen que alguna cosa es manté constant al llarg del temps. La forma més senzilla de veure les simetries són les rotacias i els reflexos, però no tots els tipus de simetries que explica la Naturalesa.
A vegades, en analitzar la descripció matemàtica d'un sistema físic és possible trobar nous tipus de simetria. Tenim un exemple històricament molt representatiu: Cas de les equacions del camp electromagnètic de Maxwell. Maxwell en analitzar les seves equacions va descobrir que els components elèctrics i magnètics no apareixien totalment simètrics. Sota una profunda sensació d'intuïció estètica, va afegir un nou tema en les seves equacions perquè fossin simètrics. Aquest nou component va aconseguir representar el camp magnètic que produeix un camp elèctric variable, el nou efecte, que va ser detectat experimentalment.
No obstant això, es va trigar més de 50 anys a comprendre la profunditat de les simetries en les equacions de Maxwell. Lorentz i Poincaré van descobrir amb sorpresa que les equacions de Maxwell eren simètriques respecte a una operació de suma d'espais i temps. Si associem temps a les tres dimensions espacials, l'estructura en quatre dimensions s'obté espaciotemporal, llavors la simetria de Lorentz/Poincaré és la rotació espaciotemporal. És a dir, existeix una relació profunda entre l'electromagnetisme i l'espai/ temps; l'espai/temps es deforma en forma simètrica quan l'observador s'acosta a la velocitat de la llum. Prenent com a real aquest fenomen tan allunyat de l'experiència tradicional, Einstein va aclarir una nova era: L'era de la relativitat.
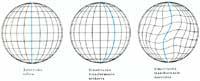
Aquesta trajectòria al llarg de la història de la ciència ens adverteix de la importància de les simetries matemàtiques per a explicar els fonaments ocults que existeixen en la naturalesa.
Renormalización i transformació gauge
Un dels obstacles més importants que se'ls presenten a l'hora de realitzar recerques teòriques per part dels físics actuals, són els termes infinits; en les equacions que els utilitzen, sovint, els valors infinits que apareixen en les magnituds físiques. Enfront d'aquest greu obstacle, l'investigador té dues vies: abandonar el model utilitzat (el que significa tornar a partir del no-res) o trobar una solució per a superar-lo. Lògicament, els físics han optat per aquesta segona via, i quan aquests infinits apareixen, renormalizan l'origen de l'escala (corresponent al punt zero) utilitzada per ells perquè el càlcul pugui continuar, desapareixent quantitats infinites. A través d'ella els teòrics descarten valors infinits.
L'electrodinàmica quàntica és una teoria que pot ser renormalizada. Però quan volem renormalizar les altres tres forces de la Naturalesa veiem que no és possible. Per això, els físics teòrics van començar a pensar que el secret de l'èxit de l'electrodinàmica quàntica quedava en la seva estructura interna, i que el seu descobriment seria aplicable a altres camps (forces).
Immediatament es comença a sospitar que aquesta estructura interna era la simetria, i el convenciment que perquè una teoria fos estable necessitava una simetria interna especial es va estendre ràpidament en ambients científics. Per això, es van començar a analitzar immediatament algunes possibles simetries especials en l'origen de les quatre forces: Les denominades “gauge”. (2)
Les simetries Gauge estan molt relacionades amb el problema de la renormalización. Aquestes simetries permeten reestimar l'escala d'alguna magnitud física. Si un sistema o teoria manté invariant el caràcter físic d'aquest sistema o teoria respecte a un tipus de canvi, tindrà simetria Gauge.

És possible reestimar l'escala d'una magnitud en tot el camp d'anàlisi; llavors estem davant una transformació global de Gauge. En el cas que els canvis d'escala siguin diferents en els diferents punts de la zona a l'hora de realitzar la normalització, la transformació de Gauge és reduïda.
Gravitació i simetries de la naturalesa
Tornarem a la naturalesa i analitzarem el fenomen polèmic i misteriós de la gravitació. Suposem que un laboratori està situat en una concentració espacial i que aquest laboratori està movent-se per l'espai en una línia recta, en la qual no existeixen forces externes. Ara suposem el segon cas. En aquest cas el laboratori s'està movent per l'espai, però el seu recorregut és corb
Passar del primer al segon cas és possible, i per a això només hem d'introduir la influència d'un camp extern. Més concretament, introduir un camp gravitatori.
La trajectòria d'un laboratori en l'òrbita d'un planeta és la mateixa que la d'un laboratori en moure's per l'espai buit. I la raó és senzilla. El recorregut corb en una òrbita compensa les forces que exerceix sobre el laboratori per la gravetat. Des d'aquest punt de vista, la gravetat és un camp compensatori mitjançant el qual es recupera la desviació del sistema respecte a la línia recta.
En aquest sentit, si el camp gravitatori introduït fora prou complex, podríem obtenir lleis físiques simètriques, encara que tinguéssim transformacions gauge reduïdes. El camp gravitatori seria el comportament de la Naturalesa per a mantenir la simetria gauge reduïda. En aquest cas, el contingut de la simetria seria la inalterabilitat de les lleis físiques quan el recorregut d'un moviment canvia arbitràriament.
Si analitzem els fenòmens físics des d'aquest punt de vista, la gravetat podria redefinir-se com l'aparició d'una simetria en la Naturalesa.

Així les coses, les quatre forces bàsiques que regeixen el comportament de l'univers serien les àrees compensatòries que la naturalesa crea per a equilibrar les simetries nocturnes reduïdes en l'estructura interna. Al seu torn, els camps de força seran la via per a imposar en l'activitat de la naturalesa les simetries gauge reduïdes en l'univers.
Si revisem les construccions físiques més generals des d'aquesta perspectiva, ens adonarem que el camp electromagnètic és la simetria nocturna més fàcil de compaginar amb la relativitat reduïda. En aquest cas correspondria als canvis en les transformacions voltaiques gauge.
Ha estat molt important constatar que el problema de la renormalización i el de la simetria nocturna estan profundament entrellaçats. En definitiva, el funcionament superperfecto de l'electrodinàmica quàntica i la seva capacitat de renormalización radica en la senzilla estructura interna del camp electromagnètic.
OBSERVACIONS :
- Entre els acceleradors de fracció actuals, el FERMILAB (Fermi National Accelerator Laboratory) és un dels més poderosos. Aquesta màquina accelera els Protons, l'energia de feix dels quals pot aconseguir els 1000 GeV. Cap a 1990 es posarà en marxa a l'URSS l'accelerador denominat UNK, obtenint una energia de 3000 GeV. Al voltant d'aquestes dates es posarà en marxa el nou FERMILAB de 5000 GeV. Per a finalitzar, cal esmentar que és el major projecte tecnològic que s'ha plantejat en l'existència humana. Aquest projecte es troba actualment a nivell de disseny. Aquest accelerador es diu VBA (Very Big Acelerator) i accelera els protons. L'energia que podria obtenir aquesta màquina seria de 20.000 GeV. Per a construir un dispositiu d'aquest tipus serà necessària la col·laboració de diferents Estats. Encara no sabem l'any de la seva posada en marxa, però sent tan gegant, l'únic lloc apropiat per a la seva construcció serà el desert. I allí ho construiran. En anglès gauge symmetries . En castellà, simetrias gauge o simetrias d'aforament.





