Mesturado V

Volvemos a ti, ese lector, era a pregunta. Lembra que esperamos as túas preguntas, xogos, etc. Anímache!

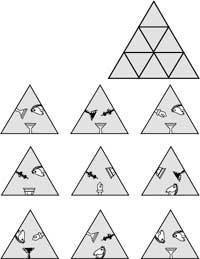
  1. Cos 9 triángulos inferiores hai que completar o superior para que as figuras dos lados que se unen formen una peza de xadrez.
  2. Pensa que un ferro AB de 500 metros está fixado nos extremos do chan.A
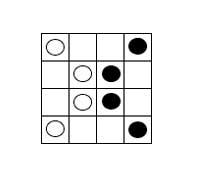
    calor do verán fai que o ferro se alargue dous metros formando un abultamiento. Considerando que o ferro se aneja simétricamente, que altura aproximada terá o abultamiento? : 10 cm, 1 metro, … Una vez respondido intuitivamente, procura calculalo.
  3. Divide o cadro adxunto en dous partes iguais, deixando dúas fichas das dúas cores, pero sen que as fichas do mesma cor tóquense entre si (nin nos lados nin nos vértices).
  4. Partindo dun dato de base chégase ao dato superior que leva 6. Paira iso hai que mover tantos pasos como puntos indica o dato, en horizontal ou en vertical (arriba ou abaixo) cada vez (non os dous á vez). Por exemplo, empezando polo dato de base 4 cara á esquerda 5,3,1,2; cara á dereita 3,5,3,3,3,2 ou cara arriba 3,5,4,6.
  5. Trátase de unir os vértices dun cadrado de 3 metros de lonxitude polo camiño máis curto. Cal é o camiño? (non é fácil).
  6. Paira a compra de 100 aves tipo 5 dispós de 100 drakmas. Un tolva vale 2 dracmas, un bufo un dracma, dous papagaitxos un dracma, tres merlos Araba un drakma e catro txolares un dracma. A compra inclúe cinco tipos de aves. Cantas compras diferentes pódense realizar?.
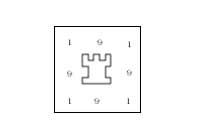
  7. 40 nenos defendían un castelo de area tal e como se ve na imaxe, é dicir, cada parte era defendida por 11 nenos. No catro primeiros tempos, catro nenos perderon os defensores e dous no cinco e últimos. Con todo, tras cada ataque cada lado do castelo era defendido sempre por 11 nenos. Sabes como?.
  8. Como formaría seis cadrados con 12 mistos se o lado dos cadrados está formado por un misto completo?
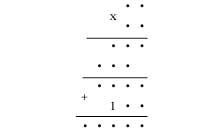
  9. Nas operacións inferiores (multiplicación e suma) cada punto é un díxito. Podes conseguir una única solución?.
  10. Nos dous partidos de damas contiguos é a quenda dos brancos e gañan.
  11. Con cifras romanas
    as dúas operacións están ben.
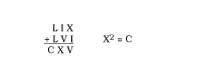
  12. A suma das cifras dun número de dúas cifras é o cadrado da raíz cúbica do número. Cal é o número?.
  13. A caixa vermella da imaxe (se non ves vermella fáltache imaxinación) ten catro caixas vermellas ou brancas. Una das 5 caixas ten un só vermello (aínda que pode ter máis vermello). Ademais, una caixa branca ten un só vermello (aínda que pode conter outros brancos) e ao mesmo tempo está dentro dun só vermello. De maior a menor que cor son as caixas?.
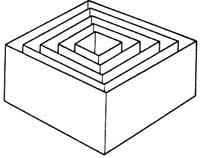
  14. O deserto está enfronte. Debes colocar o banderín a unha distancia de 4 días de percorrido. Non tes equipos especiais e só podes usalos pola túa forza. Se queres podes levarche un amigo. O banderín non presenta problemas. Con todo, existe un límite: a da auga. Cada persoa pode levar auga durante 5 días. Por iso, se viaxas só con esa cantidade de auga poderías levarche dous días e medio no deserto e volver despois. Como levarías o proxecto sen gastar auga durante 20 días e cun máximo de 3 persoas?
  15. Non asumiremos o risco de quedarnos esquivos. Observar o cubo e calcular o número de partes da superficie separadas por liñas finas. Ollo! As liñas continuas atópanse nas zonas que ven e as liñas descontinuas nas que non ven. Ten moito coidado! Os bordos do cubo non delimitan recintos. E aínda máis! A cuestión do oculista pode ser enorme.
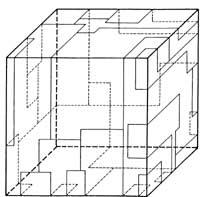
  16. Completa a imaxe para que cinco barras de aneis queden unidos entre si.
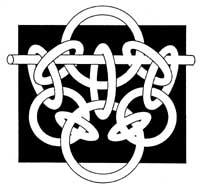
  17. Nas vilas non hai pontes. Nin túneles. As cruces só se atopan nas cidades. Cada camiño une dúas cidades, pero non pasa por outra e non cruza outra. As cinco cidades de Illa están conectadas por seis vías: Urbano a Urbano, Urbano a Urbano, Urbano a Urbano, Urbano a Urbano, Urbano a Urbano, Urbano a Urbano, Urbano a Urbano, Urbano a Urbano, Urbano a Urbano e Urbano a Urbano. O camiño que aglutinaría a Hiriño e a Urbegi sería ilegal. Todas as cidades están na costa, excepto a capital. Está no interior. Como se chama a capital de Hirikitan?.
  18. Si cinco e catro son equivalentes respectivamente ás series 9-21-11-2 e 0-4-36, a que serie corresponde una?
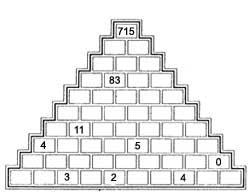
  19. Escribir un número en cada ladrillo para que sexa a suma dos números de dous ladrillos situados baixo el.
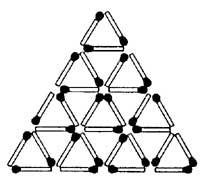
  20. Esta é una variante do xogo Nim: os xogadores, alternativamente, quitan un fósforo, desfacendo un ou varios triángulos. Por tanto, nunha xogada pódense desfacer triángulos formados por 3, 6, 9 ou 12 mistos. O gañador será o que desfaga o último triángulo. (Descoñecemento da estratexia de gañar).
  21. Tres cartas están boca abaixo, una delas marcada. Agora tes a primeira oportunidade de acertar coa marca. Ensínoche sen marca algunha das que ti non elixiches (por exemplo, se elixiches a central, una das puntas). A pregunta é si nesta segunda opción tes que seguir coa carta que elixiches ou cambiar de carta? (lembra que xa viches una carta). (Montse Hermo).

Este é, por tanto, a quinta lea. Esperamos que che guste. Non esquezas o que tiñamos ao principio. Que este apartado sexa o punto de encontro dos lectores. Até a próxima!

Babesleak
Eusko Jaurlaritzako Industria, Merkataritza eta Turismo Saila