Sota la influència de la relativitat general
Quan Einstein va publicar en 1905 la Teoria de la Relativitat Especial (TUE), el concepte que teníem sobre el temps va tornar a ser relatiu. Deu anys després, no obstant això, ens va sorprendre encara més: l'espai i el temps que coneixem... són corbs. Però de què parlava quan li va corbar?
Elhuyar. Ciència i Tècnica
front
En el número de, vam veure EBT. Llavors vam dir que EBT només serveix quan l'observador es mou a velocitat constant. Observadors amb acceleració
a)
en TC necessitem una teoria més general, la Teoria de la Relativitat General (TCE). Aquesta teoria, a més de ser més estranya que la TUE, requereix una formulació matemàtica més difícil. Per això, la regla i el rellotge
a)
veterà
Malgrat la senzillesa de trobar demostracions de la UET, les explicacions sobre EOT són molt més reduïdes. En qualsevol cas, tractarem d'acostar-se amb atenció al col·lectiu de lectura per a no espantar al lector
...
EBT i gravitació

La gravitació, una llei que explica l'atracció mútua dels planetes (i de tots els cossos amb massa), va ser ideada per Newton (veure figura 1-A), que va servir per a explicar el que es veia en la pràctica al llarg dels segles… excepte algunes excepcions. Però com ja es va comentar, la TUE exigeix una modificació de les fórmules, per la qual cosa la TUE obliga al fet que la fórmula tradicional adopti la forma indicada en la figura 1-B. No obstant això, els resultats de la nova fórmula no coincideixen amb l'experiència. Per contra, són encara pitjors que els de la fórmula antiga.
Per això, hem arribat a una situació en la qual, d'una banda, EBT no serveix per als observadors en acceleració i, per un altre, no és capaç d'explicar la gravitació. Sobre la base d'això, pensar que pot existir certa relació entre acceleració i gravitació sembla bastant lògic, i el treball d'Einstein va ser demostrar aquesta relació.
Espai/temps i TSE
Tots els esdeveniments es realitzen en un lloc i temps. Sense espai i sense temps no hi ha res, no ha ocorregut res que no hagi ocorregut en cap lloc ni en cap moment amb claredat. L'espai/temps és, per tant, la base, estructura o envàs del món.
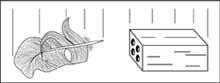
Fa temps que tot el cos que Galileu havia cedit (tant pesat com lleuger) queia amb la mateixa acceleració era conegut, però no li va donar importància.
Ara pensem que una bicicleta que recorre el carrer salta en un lloc concret. Pensarem que la causa pot ser la bicicleta, el ciclista, la carretera o el vent. Però més tard un cotxe salta en el mateix lloc, i el mateix li passa a un autobús i a un camió. Una vegada vist això, direm que la raó del salt no té a veure amb els vehicles, sinó amb la naturalesa de la base, és a dir, amb la carretera. El mateix va dir Einstein, és a dir, que la caiguda de tots els cossos amb la mateixa acceleració es deu a l'envàs, en ser espai/temps (veure figura 2).
D'altra banda, i atès que l'espai/temps és o és imprescindible perquè ocorri alguna cosa, l'espai/temps afecta a tots els cossos. Per tant, en la naturalesa no hi ha fracció lliure, i com un observador o un cos ha de ser lliure per a circular a velocitat constant, no hi ha observadors inercials (v=cte.) també. En conseqüència, no hi ha observadors privilegiats. Tots els observadors són equivalents, és a dir, hem aconseguit una relativitat total, ja que ja no hem de fer cap restricció (TEE v=cte. ens sol·licitava).
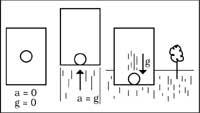
Per exemple, un astronauta crida en l'espai i cau contra una paret. No serà possible que l'home sàpiga si aquesta caiguda es deu a la inèrcia de l'acceleració del vaixell o a la gravitació d'un planeta
Però com es formula aquesta manera de ser espai/temps? I com es relaciona amb els moviments dels cossos?
Característiques espaciotemporals
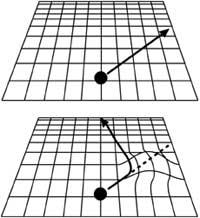
Abans hem vist que la caiguda dels cossos es deu a la forma espacial/temporal. Si aquest espai/temps és pla no afectarà. En cas de ser corbat, per contra, afectarà (veure figura 4). Per això, és el nostre espai/temps corb. Lamentablement té quatre dimensions (tres per a l'espai i una altra per al temps), per la qual cosa no podem veure aquesta curvatura. Per contra, els matemàtics no coneixen davanteres i expressen la mètrica espaciotemporal amb total facilitat. Els que dominen les matemàtiques poden mirar al quadre, però els altres millor no mirar.
Vegem ara la segona característica. En les teories antigues (inclosa la TUE, i en altres teories gravitatòries actuals), l'espai/temps era rígid, és a dir , era un recipient de successos, però sense influir en els fets. Per part seva, EOT reivindica que l'espai/temps també és un objecte dinàmic, és a dir, que els objectes i successos deformen l'espai//temps i viceversa, les deformacions espaciotemporals afecten el comportament d'objectes i successos (veure figura 5).
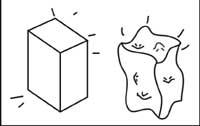
Per tant, a més de ser un espai/temps corb, també és dinàmic.
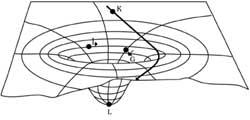
L'últim pas d'Einstein va ser identificar aquestes deformacions amb la gravitació. Va explicar més o menys que fins ara una massa atreia sense mitjans ni recursos a objectes del seu entorn. Segons Eot, per part seva, una massa deforma espaitemps i aquesta deformació condiciona les trajectòries dels objectes del seu entorn (veure figura 6).
Va donar a la teoria un reflex matemàtic a través de diverses fórmules. Aquestes fórmules relacionen la naturalesa de l'espai/temps, la curvatura i les masses i energies en joc, però són tan complicades que només les esmento en el quadre.
Conclusions
Aquestes característiques espaciotemporals generen una sèrie de conseqüències. Els més coneguts són:
- La trajectòria de la llum es corba quan passa pel lateral d'una massa, ja que la llum també és atreta per la gravitació (com es pot observar en les Figures 6 i 7).
- Com més gran és l'enregistrament, més lent van els rellotges.
- Cal crear ones gravitatòries com les que apareixen en l'aigua. ( Li necessitem perquè encara no s'han trobat).
- La conseqüència més coneguda és el forat més negre. Així que els analitzarem més a poc a poc.
Forats negres
Quan es van resoldre per primera vegada les equacions d'Einstein,
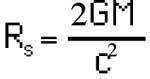
Es constata l'absència de resolució de valors. Què passava a aquesta distància? Al principi es va pensar que el cos no podia ser menor d'aquesta mesura, però després es va demostrar que una estrella podia contreure's fins a una grandària menor que aquest valor. Llavors es va entendre què demontres era R s, un límit. Qualsevol cosa (fins i tot la pròpia llum) que es trobi a una distància menor de R s d'un cos no podrà escapar i caurà contra el cos. Però com la llum tampoc és capaç d'escapar, nosaltres no podrem veure aquest cos. Per això es diu forat negre.
Exposició a ETAP
Què passaria si el nostre Sol (R s) fos capaç d'aconseguir aquesta mesura? (En principi la massa és insuficient per a aconseguir-ho). Al principi es veuria contret, cada vegada més petit. Posteriorment, a mesura que es vagi reduint, el seu color es faria cada vegada més vermell i finalment desapareixeria. Per tant, els planetes girarien al voltant de l'insignificant. De res? No, nosaltres no veuríem el Sol, però la seva massa estaria embolicada en un punt. A mesura que ens acostem a aquest punt no el veuríem, però si ens acostem a 3 km (perquè R s = 3 km per al Sol) no podríem tornar enrere. Una vegada superats els 3 km, nosaltres també (com la llum) ens quedaríem captius i tiraríem contra el punt.
Per a detectar la densitat necessària per a crear forats negres, recorda la següent dada: El R s de la Terra és d'1 cm, és a dir, si tota la Terra estigués contreta fins a una esfera de menys d'1 cm de radi, no podríem sortir d'ella ni ens veurien des de fora. O en altres paraules, la nostra Terra hauria de contreure-la fins a 1 cm per a convertir-se en un forat negre.
Cura, no obstant això, amb els viatges: el nostre cos no tindria res a veure o percebre perquè sobreviuria prou.
Boig en el món
Aquesta curvatura provocada per les masses es deu al fet que el valor G és extremadament baix (G = 6,672 x 10 -11). Però què passaria si aquest valor fos molt major? Per a començar, no podríem viure en la Terra. La seva força d'atracció seria tan gran que ens trepitjaria contra el paviment. Les estrelles tampoc il·luminarien el cel com salpicón, ja que la majoria d'elles serien forats negres. Tots els cossos que veuríem serien vermellosos. I és que aquest món de G petit es veuria com quan il·lumines una habitació amb bombetes vermelles.
També en aquest cas, per diferents motius, es produiria la paradoxa dels bessons. Si el dia de Biki, dos nascuts, portéssim un d'ells a la costa i l'altre a un cim, tornant a ajuntar-nos amb el pas del temps, comprovaríem que el primer seria jove i el segon ancià.
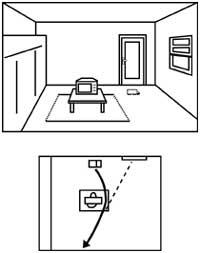
A més, tindríem una enorme dificultat per a determinar la ubicació dels objectes en funció de la nostra posició (veure figura 7).
I de tot això, al final què?
Aquests possibles exemples poden estar molt bé, però en el dia a dia no percebem en absolut les curiositats d'EBT i EOT, ni el temps relatiu ni l'espai/temps corb. I la veritat és que encara que la teoria té moltes aplicacions científiques, no hi ha grans errors a creure que el món que veiem és com el que sabem.
Sí, però nosaltres tampoc podem trencar la curiositat, no podem satisfer la fam de la causa. Qualsevol pas que ens ajudi a posar en evidència les lleis ocultes que té el funcionament del món resultarà apassionant. I és que les fantasies de l'esoterisme queden pàl·lides davant l'ET. Una vegada més, la realitat ha superat la ficció.
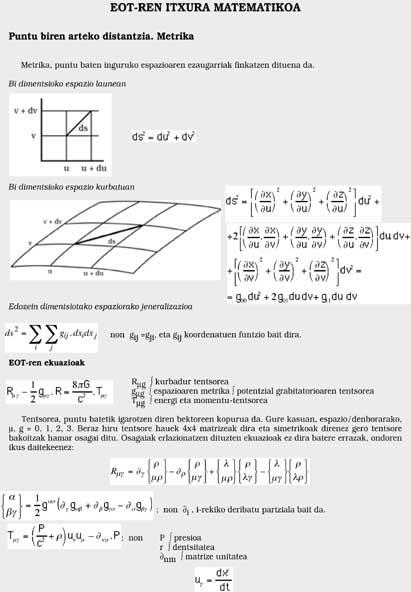

(Nota: Per a veure bé aquestes dues últimes imatges pots anar al pdf).





