Novos métodos paira mellorar a técnica de salto de altura
As técnicas de formación dos atletas cambiaron radicalmente. A principal técnica era a imitación de atletas de alto nivel, na actualidade utilízanse sistemas máis complexos como probas médicas e psicolóxicas, estudos de alimentación, análise biomecánicos, etc.
Como é sabido, a biomecánica estuda o movemento corporal mediante as leis básicas da mecánica e Leonardo dá Vinci e Galileo, XV. e XVI. Prestixiosos científicos de séculos considéranse pioneiros da biomecánica actual. Co obxectivo de dar resposta aos diferentes deportes e grazas aos avances dos computadores, esta ciencia desenvolveuse notablemente e converteuse nunha ferramenta imprescindible paira atopar os factores que inflúen na habilidade e técnica do atleta.

Baixo a coordinación do Comité Olímpico Internacional, o CEIT e outros centros de investigación internacionais realizaron análise biomecánicos de deportistas que participaron nos Xogos Olímpicos de Barcelona de 1992. A información paira a realización das análises obtívose mediante tres videocámaras. A continuación realizáronse cálculos matemáticos paira simular o movemento no computador, o que supuxo ademais de profundar na mecánica dalgúns deportes, a obtención de espectaculares animacións.
Na figura 1 pódese ver un dos saltos realizados por Javier Sotomayor, propietario da marca mundial. Este artigo pode considerarse como una continuación das investigacións realizadas entón e ademais pretende ser una axuda paira ver como se realizan este tipo de cálculos. Paira iso desenvolveremos un sinxelo modelo de análise de salto de altura. Este modelo explícanos que os movementos das diferentes partes do corpo, a dinámica muscular e as relacións neuromusculares entre si, permiten realizar movementos complicados de forma óptima e coordinada.
Salto de altura: fundamentos da técnica
Como en calquera proba de atletismo, no salto de altura hai que vencer as forzas da natureza, neste caso a da gravidade, e trátase de realizar a secuencia de movementos que hai que realizar paira superar a barra horizontal a unha altura.
A altura máxima alcanzada no salto pódese dividir en tres alturas de ataque, altura de voo e altura libre. A altura de ataque (H 1) é a altura do centro de gravidade do atleta no momento do ataque. A altura de voo (H 2) é a diferenza entre a altura máxima alcanzada polo centro de gravidade e a altura de ataque. A altura de voo só depende da velocidade vertical alcanzada polo atleta tras o ataque.
Por último, a altura libre (H 3) é a diferenza entre o listón e a altura máxima que alcanza o centro de gravidade. Pola súa banda, o valor da altura libre depende da velocidade de rotación que leva desde a posición de ataque case vertical até a posición sobre o listón, case horizontal, e dos movementos que debe realizar o atleta paira pasar sen tirar o listón. Por tanto, a altura libre depende do estilo de salto do atleta.
No desenvolvemento da técnica de salto de altura pódense distinguir diferentes estilos: tesoira, ventre, Fosbury, etc. A experiencia demostrou que o estilo “Fosbury” é o máis eficaz e utilizado maioritariamente por atletas contemporáneos. Por tanto, é o que imos analizar neste artigo.
Modelo biomecánico
O movemento que realiza o atleta no momento do salto é moi complexo e por tanto difícil de interpretar. Por tanto, o movemento debe simplificarse paira poder traballalo mellor. Con todo, as características máis importantes do movemento deben manterse para que o resultado sexa correcto.
Neste caso o atleta represéntase a través dun sistema formado por tres elementos ríxidos (patas, coxa e tronco) que se unen en dúas articulacións (xeonllo e cadeira) e o movemento do atleta débese a seis grupos musculares.
Pola súa banda, as ecuacións correspondentes ao modelo mecánico a utilizar pódense obter mediante métodos usuais na análise dinámica: Ecuacións de Newton, métodos de traballo virtual, etc.
Onde os vectores de posición, velocidade e aceleración das coordenadas que describen o sistema 0, 0, 0, son o vector que forma a forza de gravidade F G e o vector de forza muscular F M.
Cada músculo substitúese por un sistema de tres elementos. O músculo en si mesmo está formado por un elemento recapitulativo (O) que traballa paralelamente e un elemento pasivo (EP). A forza que pode exercer o músculo depende da súa lonxitude, da súa velocidade de acortamiento e da actividade muscular exercida polos nervios. O elemento abreviado ten en conta todas estas relacións, mentres que o elemento pasivo representa as características elásticas do músculo en condicións distendidas. No noso caso, o músculo atópase en serie co elemento (CE) que representa o tendón e é linealmente elástico.
Esta práctica simplifica bastante o movemento e, ademais, tense en conta a interdependencia entre a dinámica do movemento, a dinámica muscular e a relación neuromuscular.
O parámetro de entrada a este modelo é o estímulo nervioso ao longo do tempo e pode medirse experimentalmente utilizando técnicas de electromiografía (EMG). Mediante a colocación de electrodos na superficie muscular pódese obter a imaxe gráfica dos sinais eléctricos correspondentes ás activacións musculares. Neste caso, tendo en conta que os movementos do atleta son instantáneos, suponse que os músculos adquiren un gran estímulo nun curto espazo de tempo.
Formulación
Se analizamos o modelo elixido, observamos que no salto do atleta interveñen dous tipos de variables:
Condicións iniciais: ángulo inicial do corpo con respecto ao chan 0 0 , velocidade horizontal Vx 0 , velocidade vertical Vy 0 e velocidade angular w 0, todas elas medidas no momento de ataque. Os valores destas variables deben limitarse para que sexan proporcionados á capacidade humana.
Excitación muscular ao longo do tempo: os estímulos nerviosos deben situarse nun intervalo de tempo, entre o comezo do estímulo t 1 e o final t 2.
Se proporcionamos a todas estes variables valores reais correspondentes a un salto, pódese obter a simulación do salto con axuda do computador e o valor da altura superada. Por outra banda, as técnicas de optimización matemática permiten obter valores óptimos paira as condicións iniciais e os estímulos nerviosos que se atopan dentro das posibilidades do atleta.
Esta información é moi útil paira o atleta e, como non, tamén paira o adestrador. Con esta ferramenta, o atleta, ademais de coñecer as características que debe corrixir, pode coñecer a combinación de forzas musculares paira conseguir un salto óptimo.
Resultados
Na figura 7 pódese observar a simulación do salto optimizado do modelo con características medias de saltadores de altura superiores. Atleta de 1,9 metros de altura e 75 kg de peso cunha velocidade vertical en ataque de 5 m/s. Se representamos a simulación de forma gráfica, veremos que ten gran similitude co que fan os saltadores de altura superiores na realidade.
O atleta superará os 2,42 m de altura. Na táboa superior recóllense as diferentes partes da altura.
Estudo das condicións iniciais: sabendo que a altura libre é do 2,5% da altura total, pódese rexeitar este compoñente da altura. É dicir, supondo que toda a altura que superou é igual á alcanzada polo centro de gravidade do atleta, poderiamos aproximarnos á altura que superou o atleta mediante a fórmula do tiro parabólico. Por tanto, a altura obtida neste caso dependerá da altura inicial do centro de gravidade e da velocidade vertical. En todas as probas realizadas, una vez optimizado o salto, púidose confirmar que o saltador de altura utiliza a máxima velocidade vertical que pode alcanzar. Este resultado é lóxico xa que a ecuación (2) mostra que a velocidade vertical é o parámetro máis efectivo á altura superada. A dependencia da altura inicial do centro de gravidade tamén inflúe directamente, por iso é polo que se faga 0 = 90º.
A velocidade horizontal e a vertical son menos efectivas. O primeiro apenas afecta á altura alcanzada e o seu valor está relacionado coa interacción co chan en ataque, considerado como 0,5-0,6 da velocidade vertical. Pola súa banda, o valor da velocidade angular debe ser tal que o saltador de altura alcance una posición horizontal sobre o listón.
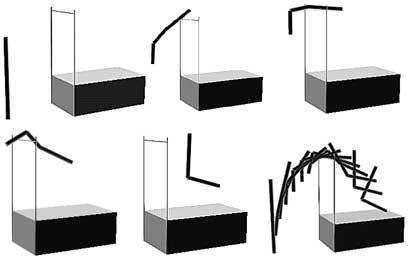
Estudo do movemento e dos músculos: o saltador de altura inicialmente recto comeza a virar; a medida que se achega ao listón, vira a cadeira e dobra o xeonllo. En canto a cadeira supere o listón, o atleta inclínase bruscamente cara ao lado contrario, subindo a coxa cara arriba. Cando a parte posterior da perna está preto da barra, pola contra, estirará as pernas. A inclinación da cadeira e o estiramento do xeonllo aseguran a seguridade do atleta ao aterrar, adoptando una posición en “L”.
A evolución das forzas exercidas polos distintos grupos musculares considerados pódese observar nas gráficas da figura 8.
Conclusións
O método de análise do movemento humano presentado neste artigo condicionará as investigacións futuras, fixando a nova base. A maior parte dos estudos realizados até o momento só tiñan en conta a dinámica do esqueleto. Aquí, pola contra, tívose en conta a complexa estrutura muscular e as relacións neuromusculares, formando un modelo simple e práctico que describe con precisión o movemento real.
Altura (m) | Porcentaxe (%) | |
Altura de ataque Altura de voo Altura libre Altura total | 1,08 1,28 0,06 2,42 | 44,6 52,9 2,5 100 |
Una vez analizados os resultados dos estudos, o salto de altura é una proba moi técnica. A altura superada, ademais de depender da forza instantánea da perna de ataque que limita a velocidade de despegamento, está influenciada por outras características como a estrutura do corpo, a elasticidade e as técnicas de coordinación de movementos. En consecuencia, pódese dicir que a forza, a potencia muscular e a preparación xeral da coordinación entre as distintas partes do corpo son necesarias paira mellorar o nivel do atleta.
Paira terminar, dicir que unha formulación deste tipo abre as portas a outros problemas de todo tipo, como o deporte, a rehabilitación ou a ortopedia.





