Hasiera »   Erreportajeak »   Sistema espazialen aro berria topografian eta geodesian

Sistema espazialen aro berria topografian eta geodesian

• Zabaldu:
• Twitter
• Facebook
• Emaila

Topografiak Lurraren ezaugarri natural zein artifizialak irudikatzea du helburu. Beraz, Lurreko edozein puntu edo elementuren informazio grafiko eta espaziala neurtu, jaso eta argitaratzeko behar diren metodo eta teknikak aztertzen ditu.

Lurreko elementuak kokatu eta irudikatu ahal izateko, topografiak Lurraren forma eta dimentsioak ezagutu behar ditu, eta horixe da geodesia zientziak eskaintzen duena.

Azken hamarkadetako aldaketak

Topografia eta geodesia alorreko lehenengo aurrerapausoak Bigarren Mundu Gerraren ostean gertatu ziren. Orduan, elektronika, mekanika, optika, matematika, fisika... asko garatu zituzten, eta horrek zientzia geomatikoen iraultza ekarri zuen (horien artean topografiarena eta geodesiarena), metodo eta tresna berriak garatu baitzituzten. Metodo horiek distantziaren eta angeluen neurketa elektronikoa egiten dute, uhin elektromagnetikoetan oinarrituz. Gerora, informatikaren garapenari esker, datu matematiko zein geografikoen kudeaketa egiteko softwareak garatu zituzten, eta lehen eskuz egiten ziren kalkulu konplexuak automatikoki egiteko aukera eman zuten.

Hurrengo iraultza sateliteen eskutik iritsi da. 70eko hamarkadatik aurrera, satelite artifizialen erabilerak onura izugarriak ekarri ditu topografian, eta, bereziki, geodesian. Izan ere, elkarrengandik oso urrun dauden puntuak zehaztasunez kokatzeaz gain, Lurraren forma, Lurraren geodinamika eta grabitate-indarraren azterketa egiteko aukera berriak ireki ditu geodesia espazialak. Zalantzarik gabe esan dezakegu metodologikoki iraultza baten aurrean gaudela: geodesia eta topografia klasikoak gaindituta, GNSS (Global Navigation Systems) deritzen sistema espazialek bide berriak ireki dituzte, bai topografiako lan arruntetan, bai eta geodesiako lan eta ikerketetan ere.

Kokapena

Sistema espazialen bidez erabiltzailearen kokapena nola zehazten den ulertzea nahiko sinplea da. Trilaterazio-metodoaren bidez kalkulatzen dira kokapen-koordenatuak (X,Y eta Z).

Trilaterazioa topografian erabiltzen den metodo arrunt bat da. Metodo horrekin, puntu baten (A puntua, esaterako) eta koordenatu ezagunak dituzten hiru puntu finkoren arteko distantzia neurtuta, A puntuaren kokapen-koordenatuak (X, Y eta Z) lor daitezke.

Sistema espazialetan, puntu ezagunak sateliteak dira, eta hargailua dagoen lekutik sateliteetara dagoen distantzia neurtuta jakiten da hargailuaren kokapena zein den. Sateliteek irrati-seinaleak bidaltzen dituzte etengabe, eta, distantzia kalkulatzeko, seinaleak satelitetik hargailurako ibilbidean igarotako denbora neurtu eta argiaren abiadurarekin biderkatzen da. Sistema pasiboa dela esaten da, hargailuek seinaleak jaso besterik ez baitute egiten. Sistema honen bidez, milioika pertsonek aldi berean jakin deakete kokapena.

Denbora neurtzeko, sateliteek zehaztasun handiko erloju atomikoak dituzte. Erloju atomikoak gai dira denbora oso zehatz neurtzeko. Hargailuen erlojuak, berriz, ez dira hain zehatzak, baina zehaztasun handia lortzera iristen dira, sateliteen erlojuen eta hargailuen erlojuen arteko diferentzia matematikoki zenbatesten baita. Zenbatespen hori posible izateko, hargailu bat gutxienez lau sateliterekiko zenbateko distantzian dagoen jakin behar da. Matematikoki, nahikoa izango lirateke hiru satelite kokapen-koordenatu (X, Y eta Z) ezezagunak lortzeko, baina laugarren sateliteak posible egiten du laugarren ezezaguna ebaztea, alegia, hargailuaren erlojuaren errorea ebaztea.

Pseudodistantzia eta fase bidezko neurketak

Hargailutik sateliteetara dagoen distantzia neurtzeko, bi metodologia daude: kode bidezko neurketa eta fase bidezko neurketa.

Kode bidezko neurketan, sateliteak, seinaleaz gain, uhin-maiztasun jakin batean modulatutako kode bat bidaltzen du. Kode horren korrelazio bidez jakin daiteke seinaleak hargailura iristeko zenbat denbora behar duen; eta datu hori argiaren abiadurarekin biderkatuz, satelitearen eta hargailuaren arteko distantzia jakitea lortzen da. Distantzia-neurketa horri pseudodistantzia deitzen zaio. Nabigaziorako hargailuek horrela ematen dute kokapena, ibilgailuetan nahiz mendian erabiltzen diren hargailuek, kasu. Metodo horren bidez, 15-30 metroko zehaztasuna lortzen da kokapenean.

15-30 metroko zehaztasuna, ordea, ez da inondik ere onargarria geodesia eta topografiarako; horietan, milimetro eta zentimetro batzuetako zehaztasuna behar da. Horregatik, kasu horietan, satelitetik hargailurako distantziak uhinaren fasearen bidez neurtzen dira. Fase bidezko neurketak uhinean bertan oinarritzen dira, eta ez uhinean modulatutako kodeetan. Eta, uhinaren uhin-luzera zentimetro gutxi batzuetakoa denez, distantzia askoz ere zehatzago neur daiteke, eta kokapen zehatza lor daiteke. Halere, oztopo garrantzitsu bat dauka fase bidezko neurketak. Hargailura iristen den seinalean uhin-desfasearen berri oso erraz jakin daitekeen arren, ziklo-kopuru osoa jakitea ez da hain erraza. Ziklo-anbiguotasunaren arazoa deitzen zaio horri. Hori ulertzeko, badago XIX. mendeko adibide on bat.

Estatu Batuetako XIX. mendeko Lautada Handietako (Great Plain) neurtzaileek honela neurtzen zituzten zelai irekiak zeharkatzen zituzten lur publikoak: harri edo hesolaz betetako gurdi batean hiru pertsona joaten ziren; batak gurdia gidatzen zuen; besteak, iparrorratz batekin, jarraitu beharreko orientazioan mantentzen zuen gurdia; eta, azkenak, gurdiaren gurpilari lotutako oihal-zati batek emandako bira-kopurua kontatzen zuen. Oihalak milia bat adina bira ematen zituenean, harri edo hesola bat jartzen zuten, eta aurrera jarraitzen zuten.

Satelite bidezko kokatze-sistema gurpilaren bira-kopurua neurtzen duen pertsonaren parekoa da, desberdintasun batekin; gurdira igotzen denean, atzean etzan eta loak hartzen du. Esnatzen denean, arduratu egiten da eta distantzia jakin nahian hasten da; badaki une horretan gurpila bira erdian dagoela, baina ez daki zenbat bira oso eman dituen. Ziklo-anbiguotasunaren kasu bera da: hartzaileak badaki desfasea zenbatekoa den, baina ez zenbat ziklo oso diren.

Ziklo-kopuru osoak software bidez kalkulatzen dira, algoritmo bidez, eta azken urteetan asko hobetu dira kalkulu horiek: denbora gutxian (segundo edo minutu gutxi batzuetan) jakin dezakete ziklo-kopurua zenbatekoa izan den. Ziklo kopuru osoaren kalkulua egiteko, algoritmo horiek ezinbestekoa dute gutxienez beste hargailu baten une bereko datuak izatea. Beraz, hargailu bakar batekin ezin daiteke pseudodistantzia besterik jakin.

Fase bidezko kokapen diferentziala

Topografian eta geodesian, fase bidezko kokapen diferentziala erabiltzen da zehaztasun handiko neurketak egiteko. Metodologia horrekin, zehaztasun izugarriz jakin daiteke bi hargailuren arteko bektore tridimentsionala (oinarri-lerroa deritzona) zein den. Bektore horren kalkulua egiteko, ezinbestean, bi hargailu topografiko-geodesikoren une bereko datuak behar dira.

Kokapen diferentzialaren oinarria da bi hargailuetara iristen diren seinaleek errore berdinak jasaten dituztela. Sateliteak 20.000 kilometro ingurura egonik, haiek bidalitako seinaleek bidaia luzea egin behar izaten dute, ionosfera eta troposfera zeharkatuz, hargailura iristeko, eta bidaia horretan hainbat aldaketa edo errore jasaten dituzte.

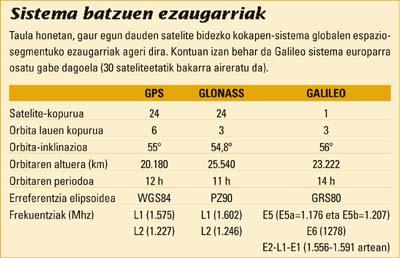
Suposa daiteke bidaia hori berdina dela bi hargailuentzat, eta, ondorioz, sateliteko seinaleak errore berdina izango duela bi hargailuetan; hala, hargailuen arteko bektorea izugarrizko zehaztasunez lor daiteke (milimetroetako zehaztasuna hamar kilometroan). Hortik abiatuta, eta bi hargailuetako bat koordenatu ezaguneko puntu batean jarrita egonik (tripode baten gainean, puntuaren gainean zehazki finkatuta), bigarren hargailuaren kokapena kalkulatzen da: bektorearen jatorriaren koordenatu zehatzak ezagunak izanik, bektorearen bigarren puntuaren koordenatuak zehaztasun handiz ezagutu daitezke.

Metodo horren bidez, kokapenaren kalkulua behaketak egin eta gero, bulegoan, nahiz unean bertan egin daiteke. Uneko kokapena lortzeari RTK (Real Time Kinematic) deitzen zaio. RTK bidez eginiko lanetan, koordenatu ezagunetan kokatzen den hargailuak (oinarri deritzona) denbora errealean bidaltzen dizkio satelitetik jasotako datuak beste hargailuari (mugikor deritzona); normalean, irrati-seinaleen bidez. Irrati seinale horrek helmen mugatua daukanez, ezin da mugikorra oinarritik gehiegi urrundu: gehienez 30 kilometro, tartean oztoporik ez badago. Hala ere, azken urteetan GPRS bidez ere bidaltzen dira oinarrian jasotako datuak, telefono mugikorren sare hedatuak aprobetxatuz.

GPS, GLONASS eta Galileo

Gaur egun, satelite bidezko bi kokatze-sistema daude erabilgarri: GPS eta GLONASS. Hirugarren bat, Galileo, eraikitzen hasiak dira.

Lehenengoa GPSa izan zen, eta Estatu Batuetako Defentsa Departamentuak sortu zuen, helburu militarrekin. NAVSTAR konstelazioak osatzen du GPS sistema. GLONASS sistema, berriz, Defentsa Zerbitzu Sobietarrak sortu zuen, eta, ondoren, Errusiako Espazio Agentziaren esku utzi zuen. Haiek, erabilera militarra emateaz gain, erabilera zibila ere indartu zuten, baina oso berandu, eta, horregatik, gaur egunean GPSa baino gutxiago erabiltzen da. Hala ere, zerbitzu militarren menpe egonik, ez batak ez besteak ez dute seinale iraunkorrik ziurtatzen.

Galileo, azkenik, satelite bidezko nabigazio-sistema europarra izango da. Sistema horrek zehaztasun handia eskainiko du, eta, kontrol zibilaren menpe egongo denez, kokapen-zerbitzu globala etengabe bermatuko du. Galileo sistema Europako Batasunaren eta Europako Espazio Agentziaren ekimena da. 30 sateliteko konstelazio bat izango da: lehenengo satelitea (eta momentuz bakarra) 2005eko abenduaren 28an aireratu zuten.

Gaur egun, gero eta gehiago dira bai GPSaren eta bai GLONASS sistemaren seinalea jaso dezaketen hargailuak. Topografian eta geodesian erabiltzen diren hargailu batzuek, esaterako, bi sistemak erabiltzeko aukera ematen dute; biak erabilita, satelite kopurua gehitu eta zehaztasuna hobetzen da.

Galileo konstelazioak horretan ere lagunduko du. Batetik, kondizio berdinetan, Galileo konstelazioko sateliteek beste bi sistemek baino zehatzago kalkulatuko dute kokapena, erloju atomiko zehatzagoak dituztelako. Eta, bestetik, GPS eta GLONASS sistemekin bateragarria izango denez, zehaztasun handiagoa lortuko dugu, satelite gehiago egongo direlako eskura: seinale gehiago jasoko direnez, doitzeen emaitzak zehatzagoak izango dira, eta, gainera, emaitzak lortzeko aukera emango du gaur egun seinalerik jasotzen ez den lekuetan, edo satelite-kopurua kokapena kalkulatzeko nahikoa ez den lekuetan.

Sistema espazialen abantailak eta etorkizuna

Satelite bidezko kokapen- eta nabigazio-sistema globalak abantaila handiak eskaintzen ditu geodesian eta topografian.

Orain arte erabili izan diren metodo klasikoen bidez, puntu baten kokapena lortzeko, derrigorrezkoa izan da puntu ezagun baten eta kokatu nahi zen puntuaren arteko ikusgaitasuna bermatzea. Satelite bidezko kokapen-sistema globalek, berriz, ikusgaitasunik ez duten puntuen arteko kokapena lortzeko aukera ematen dute; izan ere, hamarka edo ehunka kilometroko oinarri-lerroak lor daitezke, zentimetroetako zehaztasunarekin. Horretaz gain, orain arte ez bezala, satelite bidezko kokapen-sistema globalei esker, edozein klima-egoeretan egin daitezke neurketak.

Topografiaren alorrean, jasotzeak egiteko garaian, emankortasuna izugarri handitu da satelite bidezko sistema erabiliz egindako lanetan. Topografia arruntean bi pertsona behar dira lanak egiteko; satelite bidezko kokapen-sistemak erabiliz, berriz, pertsona bakar batek egin dezake lana, eta, gainera, eguneko puntu gehiago hartu.

Mugak ere badituzte, hala ere. Handiena da sateliteen seinalea oztopatzen duten lekuetan lan egitea: gaineko oztopoek, eraikinek eta zuhaitzek adibidez, sateliteen seinalea ezereztatzen dute, eta, askotan, ezinezkoa izaten da kokapena lortzea. Etorkizunera begira, baina, Galileo sistema erabilgarri denean, satelite gehiago izango direnez, hainbat tokitan gainditu ahal izango da muga hori.