Naturaren seme ezkutuak
Ikertzailea eta irakaslea
Euskal Herriko Unibertsitateko Informatika Fakultatea

Guk, orri hauetan, mendeetan zehar ongi ezkutatuta egon diren zulo beltzak aztertuko ditugu. Nola aurreikusi ziren, beren existentziaren onarpena, haiei buruz gaur egun dakizkigun hainbat gauza, eta, noski, etorkizunari begira irekitzen dituzten ateak. Baina hori guztia behar bezala ulertzeko, lehenik eta behin Einsteinen Erlatibitatearen Teoria Orokorra azaldu behar dugu (1. eranskina), hari esker jaio baitzen oraindik amaitu gabe dagoen bidaia luze honi.
Zulo beltzen jaiotza
Izar baten heriotzan, indar grabitatorioa presio termikoari gailentzen zaionean, izarra inplosio grabitatorio batean amiltzen da. Masa nahiko handia badu, gutxi gorabehera Eguzkia baino bi aldiz handiagoa, inplosioaren amaieran, zulo beltz bat jaioko da.
1916an, Karl Schwarzschildek, izarren inguruko espazio-denboraren geometria nolakoa zen argitu zigun. Kalkulu horietaz baliatuz, Robert J. Oppenheimerrek inplosionatzen ari zen izar baten itxura zein zen jakin nahi izan zuen. Baita lortu ere. Horrela, nahi dugun erreferentzia-sistematik izarraren inplosioak zein itxura duen jakin dezakegu. Has gaitezen izarrarekiko bere kanpoaldean geldirik dagoen behatzaile batekin. Kontuan izan beti distantzia berari eutsi behar diola, izarrerantz amildu gabe.
Izarra uzkurtzen doan neurrian, bere inguruko espazio-denboraren kurbadura areagotu egingo da. Ondorioz, izarrak igorritako argiak gorrirako desplazamendu bat jasango du, hots, geroz eta uhin-luzera handiagoko argia igorriko du. Hori logikoa da, kurbadura handiagotzen denean, denboraren fluxua moteldu egingo baita izar barruan. Beraz, atomoek igortzen duten argiaren maiztasuna txikiagoa izango da, eta, noski, uhin-luzera handiagoa.
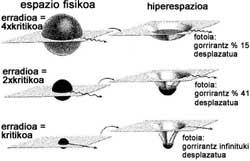
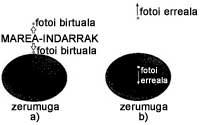
Halako batean, izarraren erradio jakin batean, argia infinituki desplazatuko da gorrirantz, hots, existitzeari utziko dio. Momentu horretan, gure izarra zulo beltz bat bilakatu da, argiak ere ihes egin ezin dion objektu arraro bat. Erradio horri erradio kritikoa deritzo (1. irudia). Gure behatzailearentzat, argiaren maiztasuna nulua izateak inplikazio sakon bat dauka: izarraren gainazalean denboraren fluxua izoztu egin da! Izarra uzkurtzen doan heinean, inplosioa moteltzen joango da, eta erradio kritikoan geldituko da. Horrela, kanpoko behatzaile horrek ez du sekula izarra guztiz uzkurtzen ikusiko.
Demagun orain izarraren barruranzko mugimenduan dagoen behatzaile bat dugula. Horren arabera inplosioa ez da erradio kritikoan gelditzen. Aurrera jarraitzen du, izarraren masa guztia bolumen nulu batean bildu arte. Momentu horretan gertatzen diren fenomenoak gure ulermenetik nahiko urrun daude gaur egun ere. Hala ere, aurrerago saiatuko gara singularitate deritzon puntu hori aztertzen.
Emaitza horiek, arras arraroak edonorentzat, ez ziren berehalakoan onartu fisikarien artean. Oppenheimerrek izarren barneko faktore asko arbuiatu zituen bere kalkulua errazteko asmoz. Horrela, bere izarrak ez zuen biratzen, presio termikorik ez zuen, erreakzio nuklearrik ere ez... asko ziren faktore horiek zulo beltzen sorrera ekidingo zutela pentsatzen zutenak.
Zalantzak zalantza, 25 urte geroago eginiko ordenagailu bidezko simulazioetan, Oppenheimerrek aurreikusi zuena gertatzen zela baieztatu zen, jada ikusi ditugun ondorioekin. Hala eta guztiz ere, oso zaila da onartzea bi behatzaileren arteko ikuspuntua horren ezberdina izan daitekeela, eta horrela gertatu zitzaien oraindik ere fisikari askori. Batzuek esaten zuten mekanika kuantikoaren eta erlatibitate orokorraren elkarketak inplosio hori etengo zuela, baina gaur egun ere urrun samar ikusten da grabitate kuantikoaren teoria desiratu hori.
Errepasa ditzagun ikusitako kontzeptuak. Erradio kritikoa zulo beltzaren erradioa da. Singularitatea zuloaren zentroa dela esan dugu. Zulo beltza hasten den lekua, kanpoaldetik begiratuta, gertakarien zerumuga da. Zerumuga zeharkatzen duen oro, betiko zulo beltzean harrapatua gelditzen da, irteteko eta seinalerik bidaltzeko aukerarik gabe; hitz batean, unibertsotik isolatzen da. Horixe da, beraz, zulo beltz baten. irudia, oraingoz bederen.
Zuloen ezaugarri nabarmenenak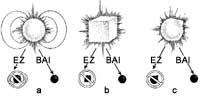
Zulo beltzek ez dute ilerik
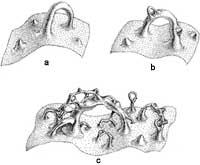
Horrela da, bai, zulo beltzak burusoilak dira. Horrek esan nahi du zulo beltz bat osatu aurretik genuen izarrari buruzko informazioa galdu egiten dela inplosioa gertatzean. Informazio hori, ilea deitzen dioguna, izarraren formari, bere eremu magnetikoari eta abarri buruzkoa da. Izarra edonolakoa delarik ere, bere inplosioak zerumuga esferikoko zulo beltz bat emango du beti (2. irudia). Hala ere, zulo beltzak hiru ezaugarri gordeko ditu: izarraren masa, karga elektrikoa eta momentu angeluarra. Ezaugarri horiek ezin dira erradiazio moduan askatu inplosioan, beraz, zulo beltzak, behin eratu ondoren, gorde egiten ditu. Bestelako ile guztia erradiazio moduan askatuko da inplosioan zehar (3. irudia).
Horrek guztiak ondorio harrigarri batera garamatza: zulo beltz bat deskribatzeko hiru propietate nahikoak dira: masa, karga elektrikoa eta momentu angeluarra. Hori ez da posible beste edozein objektu makroskopikorekin, hala nola, izarrak, planetak edo pertsona bat. Sinpletasun hori oinarrizko partikuletan bakarrik topa dezakegu. Batzuek analogia hori ez dute bere horretan utzi, baina horri buruz geroago mintzatuko gara.
Espazioko zurrunbiloak eta haien energia
Zulo beltzek duten biratzeko gaitasunak beste ondorio txundigarri horietariko batera eramango gaitu. Dirudienez, zuloa biraka ari den heinean, bere inguruko espazioari eutsi eta berekin batera birarazten du. Horrela, espazioan zurrunbilo bat sortzen da, airean sortzen direnen oso antzekoa
1969an, Roger Penrose-k ikusi zuen, zurrunbiloaren barnean zuloaren errotazio-energia metatzen dela. Eta zurrunbiloa zerumugaren kanpoaldean dagoenez, energia hori kanpoko izakiek erabil dezakete. Gezurra badirudi ere, izugarrizko energia-kantitateei buruz mintzo gara. Abiadura maximoan biraka dabilen zulo beltz batek eguzkiaren erregai nuklear guztiak baino 48 aldiz energia gehiago eman dezake! Agian etorkizuneko zibilizazioren batek asmatuko du nola erabil daitekeen energia hori guztia eta buruhauste asko konponduko ditu.
Zulo beltzak lurrindu egiten dira
Hasieran nahiko argi esan dugu zulo beltzetatik ezin duela ezerk alde egin. Behin zerumuga zeharkatzen dugunean, ezin gara berriro ere kanpoaldera itzuli. Hala ere, 1974an, uste guztien aurka, Stephen Hawkingek erakutsi zigun zulo beltzek erradiatu egiten dutela! Mekanika kuantikoaren eta erlatibitate orokorraren elkarketa partzial bat erabiliz, ondorio harrigarri horretara iritsi zen. Baina, nola da hori posible? Azalpenak ulertzeko, lehenik eta behin kuantikaren funtsezko kontzeptu bat ulertu behar dugu: hutsunearen fluktuazio kuantikoak.
Kontzeptu horren arabera, hutsunean, eremurik eta materiarik gabeko espazio-zatian, fluktuazio batzuk sortzen dira (2. eranskina). Espazioko zati batzuek energia positiboa hartu eta beste zati batzuk negatiboan uzten dituzte, modu ausazko eta zehazgabean. Baina batez besteko energia beti nulua da. Hutsunean energia-trukeak gertatzen dira, beraz.
Partikulen ikuspuntutik, fluktuazioak partikula-antipartikula birtualen bikoteen sorrerarekin uler daitezke. Hutsunean, adibide gisara, momentu batean elektroi bat eta antielektroi bat sor daitezke, espazio-zati bat energia negatiboarekin utziz. Baina segundo gutxiren buruan, elkar deuseztu eta energia itzultzen diote espazioari. Horrela, batezbestekoa beti nulua da. Egia esan, partikula horiek ez dira errealak baina, nahikoa energia emanez gero, erreal bilakatzen dira. Energia hori, noski, beren uhin-luzeren araberakoa izango da. Uhin-luzera handiagoek energia gehiago beharko dute erreal bihurtzeko, eta alderantziz. Eta hor dago gakoa.
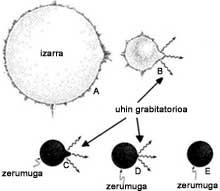
Zulo beltz baten zerumugaren inguruan, fluktuazio kuantikoak gertatzen dira. Demagun bi fotoi sortu direla, fotoia bere buruaren antipartikula baita (5. irudia). Fotoi horiek elkarrengandik urrun daitezke eremuaren energiak balio positiboa hartu duen espazio-zatian badaude. Zati hori nahiko handia bada, gutxi gorabehera zerumugaren perimetroaren antzekoa, bi fotoiak perimetroaren laurden bat urrun daitezke.
Kontuan izanik zerumugaren inguruan grabitatearen intentsitatea oso bortitza dela, fotoi horiek energia asko jasoko dute grabitatearen azelerazioari esker. Energia hori nahikoa izango da bi fotoiak erreal bihurtzeko eta elkarrengandik askatzeko.
Fotoi bat zerumugan erori eta desagertuko da, baina besteak alde egitea lortuko du, eta berarekin eramango du zulo beltzaren masaren zatitxo oso-oso txiki bat. Bai, berak hartu duen energia zuloaren eremutik hartu du, eta energia eta masa azken finean gauza bera direnez, zuloaren masa berarekin eraman du. Horrela, poliki-poliki, zulo beltza bere masa galtzen joango da eta zerumugaren azalera murriztu egingo da, azkenik zulo beltza desagertu arte! Gure zulo beltza lurrindu egin da erradiazio pila bat utzita.
Hala ere, prozesu hori zeharo motela da. Zulo beltz arrunt batek, bi eguzki-masakoa adibidez, 1,2x10 67 urte behar ditu lurrintzeko! Urte-kopuru hori handiagoa da zuloaren masa handiagoa den neurrian.
Singularitateak eta grabitate kuantikoaren teoria
Lehenago ere aipatu ditugu singularitateak, zulo beltzen zentroan dauden puntu arraro horiek. Jarraian, haien inguruan orain arte jakin ahal izan duguna ulertzen saiatuko gara. Ez da asko, baina oso korapilatsua da.
Oppenheimerren ekuazioek argi adierazten zuten singularitatea dentsitate infinituko eta bolumen nuluko puntu bat zela, hots, izarraren materia guztia puntu adimentsional batean bildurik. Puntu horretan, espazio-denboraren kurbadura infinitua bilakatzen da eta, gainera, espazio-denbora bera bukatu egiten da. Ez dago ezer singularitatearen beste aldean.
Infinitu horiek guztiak ez dira oso seinale erakargarriak fisikarientzat. Horregatik, askok uste dute singularitatea egoki deskribatzeko erlatibitate orokorra ez dela nahikoa. Fisikariak grabitate kuantikoaren teoriaren bila dabiltza jo eta ke, singularitatea behar bezala azal dezakeen ikustearren. Haien arabera, mekanika kuantikoa erlatibitatearekin behar bezala elkartuz, singularitatean ezingo litzateke grabitatea infinitu bilakatu, kuantikak ez luke horrelakorik baimenduko.
Gaur egun, ordea, ez daukagu horrelako teoriarik. Elkarketa partzial batzuk lortu dira, zulo beltzen lurrinketan ikusi bezala, baina grabitate kuantikoaren teoria osoa urrun dago. Badirudi oraingoz supersoken teoria dela helmuga horretara heltzeko hautagairik onena, baina guk ez dugu hemen horren inguruan gehiegi hitz egingo (3. eranskina). Horren ordez, dakigunarekin singularitateen ulermen-traza batzuk hartuko ditugu.
Singularitate-mota guztien artean, errealitatera gehien hurbiltzen dena BKL singularitatea izan daiteke. Azken hurbilketen arabera, singularitate horretan espazio-denbora hautsi egiten da. Espazioa eta denbora independente bilakatzen dira berriro, are gehiago, denbora desagertu egiten da. Une horretan, gertakari bat bestea baino lehenago gertatu denik ezin dugu esan, noiz bezalako kontzeptuek ez dute balio. Espazioa ere ez da guk ezagutu bezalakoa. Apar ausazko eta ezin definitua bihurtzen da, olatu bat lehertzen denean ikusten dugun aparra bezalakoa. Probabilitateak menderatuta, inork ezin du esan nolako itxura duen, itxura konkretu batzuk izateko duen probabilitatea bakarrik ezagutzen baitugu (6. irudia). Espazioa apar kuantiko bilakatzen da.
Baina, lehen esan dugun bezala, singularitateen ulermena oraindik ere ez da batere ona. Beraz, oraingoz alde batera utzi eta zulo beltzek ematen dizkiguten beste aukera batzuk aztertuko ditugu.
Denbora-makinak: fikzioa ala errealitatea?
Edonoren burutik pasatu da denboran zehar bidaiatzeko aukera, ezta? Loteriaren zenbaki irabazleak ikusi eta gure papertxoan idatzi diru pilo bat irabazteko. Ametsak azken finean. Edo ez?

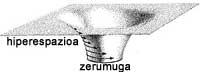
Erlatibitate orokorraz baliatuz, denboran zehar bidaiatzeko aukera batzuk badaudela ikusten da. Giltzarria zizare-zuloetan daukagu. Zizare-zuloak espazioko bi puntu konektatzen dituzten hiperespazioko bidezidorrak dira (7. eta 8. irudiak). Bidezidor horiek konektatzen dituzten bi puntu horietan singularitate bana egoteagatik sortzen dira, baina egia esan, espazioaren forma egokia izan behar dugu, eta hori kasualitate handiegia da. Hala ere, teorian posible da.
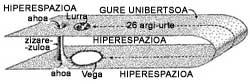
Demagun, beraz, zizare-zulo bat sortu dugula. Orain, arazoa irekita mantentzean datza, zulo horiek berehala deusezten baitira erradiazioaren ondorioz. Baina, beste behin, aukera bat badaukagu: zuloa material exotikoa deritzonaz zeharkatzea. Material horren ezaugarri nagusia da, argi-izpi batetik ikusita, energia-dentsitate negatiboa duela. Arraroa badirudi ere, dentsitatea kontzeptu erlatiboa da, eta posible da material hau existitzea. Zulo beltzen inguruan dauzkagun fluktuazio kuantikoak, hain zuzen ere, exotikoak dira.
Zulo horiek espazio-denboraren kurbaturen ondorio direnez, denbora-fluxua ez da berdina horien barnean eta kanpoan. Ezaugarri hori da denbora-makina mota bat egitea ahalbidetzen diguna. Makina hori zizare-zuloen ahoen abiadura ezberdinetan oinarritzen da. Har dezagun aho bat, joan gaitezen argiaren inguruko abiaduraz 6 ordutan eta, gero, itzul gaitezen berriro beste ahoa utzitako lekura. Bigarren ahoarekin zegoen gure lagunarentzat, gure 12 orduko bidaia 10 urteko bidaia izan da erlatibitate bereziaren arabera. Beraz, bi ahoak Lurrean daudenean, bidaiatu duen ahotik begiratuz gero, 10 urte atzeragoko gauzak ikus ditzake; eta ahoan sartzen bagara beste aldetik irteteko 10 urte atzera bidaiatu dugu! Eta, noski, 10 urte atzera eginda gero, lagunen bati etorkizunera bidaiatzeko gonbita luza diezaiokegu, irten berri garen ahoa zeharkatuz. Kontu izan zizare-zuloa ez dela denbora-makina bihurtzen aipaturiko bidaia bukatu arte.
Orain, ordea, galdera bat planteatu behar dugu: utziko al digu naturak denbora-makina bat egiten? Galdera horren erantzuna, beste behin, grabitate kuantikoaren teoriak emango digu. Hala ere, gaur egun dakigunarekin, badirudi ez dela posible horrelakorik. Zizare-zulo batean dauden fluktuazio kuantikoek, dirudienez, zuloa deuseztu egiten dute hori denbora-makina bihurtu baino zertxobait lehenago.
Hawkingek, ondorio posible hau zabaldu egin du: haren ustean, fluktuazioek mota guztietako denbora-makinak (horiek ez baitute derrigorrean zizare-zuloetan oinarriturik egon behar) deuseztuko dituzte sortu baino instant bat lehenago. Deusezte hori nola gerta daitekeen ez dugu azalduko, baina esan beharra dago, gaur egun, fisikari gehienak Hawkingen iritzi berekoak direla. Egin diren kalkuluek ez dute bestelako interpretaziorik onartzen, baina oraindik ere grabitate kuantikoaren teoriak du azken hitza. Beraz, ameslariek badute heldulekurik beraien iritziei eusteko. Nork jakin?
Ikerkuntzarentzat bide berriak
Zulo beltzen inguruan esan dugun guztiak bide berriak irekitzen ditu bai behatzaileentzat, baita teorikoentzat ere, hots, ikerketa berrientzat. Unibertsoaren behaketaren ondorioz, hainbat objektu ezezagun aurkitu dira: quasarrak, pulsarrak, erradiogalaxiak… Guztiak teknologiaren aurrerakadari esker ezagutzen ditugu, baina zulo beltzen ulermen teorikoa heldu arte ezin ziren ongi azaldu. Gaur egun, quasarrak eta erradiogalaxiak, esaterako, zulo beltzen bitartez azaltzen dira.
Fisikarien beste erronka handia singularitateen behaketarena da. Nahiz eta Penrosen zentsura kosmikoak singularitate biluzirik ez dagoela esaten duen, bada aukera bat zerumugarik gabeko singularitateak topatzeko. Hawkingen esanean, zulo beltz bat lurrintzean, ez da guztiz desagertzen. Prozesuaren amaieran, zerbait gelditzen da. Ez dakigu ziur zerbait hori singularitate biluzia ote denentz. Hala ere, hori behatu ahal izateko, Big-Bang-aren garaian sorturiko minizulo beltzak dira aukera bakarra. Horien lurrintze-denbora kalkulatuz, gaur egun amaitu behar lukete prozesu osoa. Beraz, astro berezi horiek behatzen hasiak dira hainbat astronomo.
Dena dela, zulo beltzek hainbat misterio argitu dituzte. Aipatu ditugu erradiogalaxiak eta quasarrak. Gure galaxiaren zentroan dauden izarren translazio-abiadura ikaragarriak azaltzeko ere, zulo beltz erraldoiak erabiltzen dira. Baina zulo beltzen gauzarik interesgarriena irekita utzi dituzten misterio berriak dira. Singularitateak, denbora-makinak, hiperespazioko bidaiak... etorkizunerako erronka handiak utzi dizkigute. Eta hori guztia zuzenean behatu ezin izan diren astroek eskainita, zulo beltzek, hots, naturaren seme ezkutuek.
| Einsteinen oparia (1. eranskina) Erlatibitatearen Teoria Orokorra grabitatea deskribatzen duen teoria bat da, 1916an Einsteinek argitaratua. Bere ekarpenen barne daude argiaren desbideratzea izar baten inguruan pasatzean, denboraren moteltzea, Merkurioren perihelioaren desplazamendua, eta, nola ez, guri interesatzen zaizkigun zulo beltzak. Erlatibitatearen Teoria Bereziak erakutsi zigun espazioa eta denbora erlatiboak direla, hots, abiadura ezberdinez bidaiatzen duten behatzaileek luzeren eta denbora-tarteen neurketa ezberdinak egingo dituztela. Hala ere, Hermann Minkowski konturatu zen bezala, unibertsoko fenomenoak azken finean gertaerak dira. Eta gertaera bat deskribatzeko lau zenbaki behar ditugu: hiru bere espazioko posizioa adierazteko eta bat gertatu den unea zehazteko. Gure mundua lau dimentsioko espazio-denbora baten bitartez deskriba dezakegu. Espazioa eta denbora beren kasa erlatiboak badira ere, espazio-denbora absolutua da. Hots, edozein behatzailek, edozein delarik ere bere higidura-egoera, espazio-denborako tarte berdinak neurtuko ditu bi gertakariren artean (I. irudia). Hori oso baliotsua izango da erlatibitate orokorra formulatzerako garaian. Ikus dezagun zergatia. 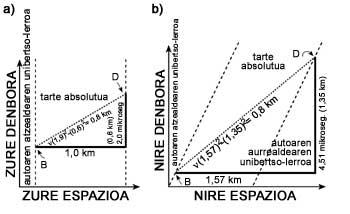 I. irudia. a) Zure espazioan kilometro bateko luzera duen auto batean bidaiatzen ari zara 162.000 km/s-ko abiaduraz, nirekiko. Zure denbora-tartean, argi bat pizten da lehenik autoaren atzealdean (B gertaera), eta 2 mikrosegundoren ondoren, beste argi bat pizten da aurrealdean (D). Bi gertaeren tarte absolutua 0,8 km da zuretzat (espazio-denboran, denbora ere km-tan neurtzen da, eta balio horiek parentesietan agertzen dira). b) Zu autoan zoazen bitartean, ni kalean nago, zuri begira. B eta D gertaeren arteko nire espazio-tartea 1,57 km-koa da eta denbora-tartea, 4,51 mikrosegundokoa. Hala ere, tarte absolutua berdina da: 0,8 km. Giltza marea-indarretan dago. Bai, itsasoko mareak sortzen dituzten indar berdinak. Newtonen grabitatearen teoria jarraituz, espazioaren puntu bakoitzean eremu grabitatorioak intentsitate ezberdinak dituelako azaltzen dira indarrok. Baina Newtonen azalpenek ez dute balio indar horiek ongi ulertzeko. Bere teorian grabitatearen aldaketa distantziarekiko agertzen da giltzarritzat, baina zer distantzia? Nork neurtua? Espazioa erlatiboa baita. Beraz, Lurrera erortzen ari den astronauta baten egoera ez da berdina izango berak deskribatuta eta guk Lurretik ikusita (II. irudia). Garbi dago azalpen horrek ez duela erlatibitate-printzipioa betetzen; beraz, beste zerbaiten bila hasi beharrean gaude. 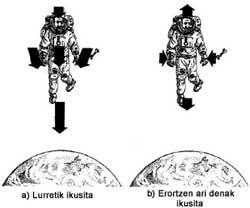 I I. irudia. Geziek indarren norabideak eta intentsitatea adierazten dituzte. Saia gaitezen honi irtenbide bat aurkitzen. Demagun lau bolatxo hartu ditugula eta Lurretik urrun aske utzi ditugula erronbo-itxuran utziz (III. irudia). Lurrera gerturatzen doazen neurrian, eremuaren eragina nabarmenagoa egingo da, eta beren ibilbide zuzenak aldatu egingo dira. Ibilbideak kurbatuak bilakatzen dira eremuak eragiten dienean. Hemendik, Einsteinek ondorioztatu zuen marea-indarrak espazioaren kurbaduraren erakusgarri zirela. Baina erreferentzia-sistema batean espazioaren kurbadurak beste batean denboraren kurbadura ere badakar, espazioa eta denbora oso lotuta baitaude. Arazo handia da hori. Infinitu erreferentzia-sistema egon daitezkeenez, abiadura eta azelerazio ezberdinekin, infinitu espazio eta denbora kurbatu dauzkagu! Izugarrizko anabasa! 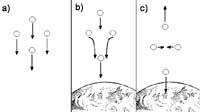 III. irudia. a) Lau bolatxo erronbo-forman jarriak eremurik gabeko espazio hutsean. Geziek beren ibilbidea erakusten dute. b) Lurrera gerturatzean beraien ibilbidea nola aldatzen den agertzen da. Goiko eta beheko bolatxoak urruntzen diren bitartean, ezker-eskuin bolatxoak gerturatu egiten dira. Geziek Lurreko behatzaile batek ikusiko lituzkeen bilbide kurbatuak adierazten dituzte. c) Aurreko kasu bera da, baina bolatxoekiko geldiunean dagoen behatzaile batek ikusia. b) eta c) kasuetan agertzen dira ongi behatzaileek ikusten dituzten kurbadura ezberdinak. Hemen agertzen zaigu, ordea, Minkowskiren espazio-denbora absolutua. Espazioaren eta denboraren kurbadurak, bakoitza bere aldetik hartuta, behatzaile bakoitzarentzat ezberdinak dira; espazio-denboraren kurbadura, ordea, denontzat bat eta bakarra izango da. Horrek, zalantzarik gabe, lana asko errazten du, baina gure ulermena pixka bat lausotzen, espazioa eta denbora bakoitza bere aldetik ikusten ohituak baikaude. Komeni zaigu, beraz, behatzaileek espazioa eta denbora nola ikusten dituzten jakitea eremu grabitatorio baten inguruan.
Demagun eremu oso indartsu batean, behatzaile bat, O, zentrotik gertu dugula, eta bestea, K, urrun, eremuaren eragina ahula den lekuren batean. O-rentzat espazioak ez ditu Euklideren geometriaren legeak errespetatuko. Hots, bi zuzen paralelo marrazten hasita, beti topatuko du punturen bat elkar moztuko dutena. Bere espazioa esfera baten gainazala bezalakoa litzateke, espazio kurbatu bat. K-rentzat, aldiz, eremuaren eragina oso txikia denez, espazioa ia-ia laua izango da. Euklideren legeek bikain funtzionatuko dute bere erreferentzia-sisteman. Denborak ere pairatzen du grabitatearen eragina. Horrela, O-ren erlojua, K-ren erlojua baino motelago joango da, hau da, eremuaren sorburutik gertuago gauden neurrian, denbora-tarteak luzeagoak dira. Deskribatu berri dugun modu honetara ulertu behar da espazioaren eta denboraren kurbadura, bakoitza bere aldetik hartuz gero. Teoria horren azken pausoa espazio-denboraren kurbaduraren kausak aztertzea da. Azkar ondorioztatzen da unibertsoan dauden masek zehazten dituztela kurbaduraren nondik norakoak. Masa handiagoentzat, kurbadura bortitzagoak, eta, ondorioz, eremu indartsuagoak (eranskina). Hori da, beraz, Erlatibitatearen Teoria Orokorrak dioena, modu orokor batean.
|
| Fluktuazio kuantikoen azalpena (2. eranskina) Fluktuazioak Heisengebergen ziurgabetasun-printzipiotik ondorioztatzen dira. Honek dio partikula baten posizioa eta momentua ezin direla guztiz zehaztu. Hau da, partikula baten posizioa zehatz-mehatz aurkitzen badugu, momentuaren ziurgabetasun handi bat sortuko dugu, eta alderantziz. Beraz, bi gauzak ez dira posible aldi berean. Momentu lineala partikularen masaren eta abiaduraren arteko biderkadura da. Horrela, espazio guztiz hutsean, zati bat aztertzen hasten garenean, tarte bat finkatzen dugu. Zehaztapen hori egiteagatik soilik, hutsunean momentuaren ziurgabetasun bat sortu dugu, posizioaren edozein zehaztapenek ondorio hori baitakar. Momentua ezin da, beraz, zero izan, hots, masa eta abiadura daukan zerbait sortuko da hutsunean. Kuantikan uhinak eta partikulak gauza bera direnez, partikula-antipartikula ikuspegia edo eremu-uhinen ikuspegia erabil daiteke fluktuazio horiek azaltzerako garaian. Gure kasuan, lehen aukera errazagoa denez, hortik jo dugu, baina momentuaren ziurgabetasuna uhin moduan ere uler daiteke. Momentuaren ziurgabetasunak zuzenean inplikatzen du fluktuazioak zehazgabeak eta ausazkoak izatea. Eta, azkenik, espazio-zati handiagoentzat, fluktuazio ahulagoak. Orokorrean, gure bizi arrunteko eskaletan, fluktuazioek ez dute eraginik, oso-oso ahulak dira. Partikula birtual bat erreal bihurtzeko izugarrizko energia beharko genuke. Energia horiek posible dira zulo beltzen eremu grabitatorioengatik eta horregatik dira fluktuazioak aintzat hartzeko fenomenoak. |
| Supersokak eta zulo beltzak (3. eranskina) Eranskin hau supersoken inguruan zerbait dakitenei zuzendua dago, beren jakin-mina pixka bat asetzeko. Lehenago aipatu dugu zulo beltzen eta oinarrizko partikulen arteko antzekotasuna. Analogia horrek supersoken teoriarekin hartzen du bere indar handiena. Horren arabera, dimentsio kiribilduetan hiru dimentsioko soka batek (hiru-brana bat) esfera bat inguratzen duenean, zulo beltz baten eremu grabitatorio berdina sortzen du. Makroskopikoki zulo beltz bat da. Esfera hori txikitzen doan neurrian, bere joera hori baita, zuloa masa galduz doa eta, azkenik, masa gabeko zerbait bihurtzen da. Zerbait hori, espazioaren topologia aztertuz, oinarrizko partikula bat dela ikusten da. Interesgarria litzateke jakitea hori ote denentz zulo beltzen lurrinketaren azken fasea. Baina ez dakigu. Bestalde, supersokek zulo beltzen hainbat propietate azaltzea lortu dute, hala nola, beren entropia. Baina benetan grabitate kuantikoaren teoria zuzena dela frogatzeko lekurik onenean, hots, singularitateetan, oraindik ez du emaitzarik eman. Beraz, singularitateei buruz orain arte ikasi duguna ez da aldatzen. Gaur egun, azalpen onena, gezurra badirudi ere, guk emandakoa da. |
BIBLIOGRAFIA
- Hawking, S. W. eta Penrose, R. (1996).
La naturaleza del espacio y el tiempo.
Editorial Debate, S.A. (1998). - Jean-Pierre Luminet (1987).
Agujeros negros.
Alianza Editorial, S.A. (1991). - Einstein, A. (1916).
Sobre la teoría de la relatividad especial y general.
Ediciones Altaya, S.A. (1998). - Davies, P.
En busca de las ondas gravitatorias.
Salvat Editores, S.A. (1995) - Weinberg, S. (1976)
Unibertsoaren hasierako hiru minutuak – Unibertsoari buruzko ikuspegi modernoa.
Gaiak argitaldaria (1993). - Thorne, Kip S.(1994).
Agujeros negros y tiempo curvo. El escandaloso legado de Einstein.
Crítica (1995). - Hawking, S. W. (2001).
El universo en una cáscara de nuez.
Editorial Planeta, S.A. (2002) - Hawking, S. W. (1988).
Historia del tiempo. Del Big Bang a los agujeros negros.
Alianza Editorial, S.A. (1995).





